Olá seja bem vindo ao meu mais novo artigo
Segue abaixo o artigo publicado do autor John Tukey (1949),
https://www.jstor.org/stable/3001913
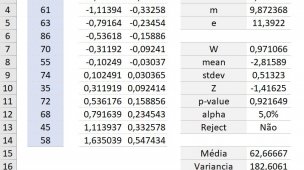
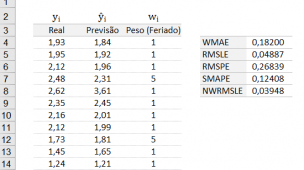
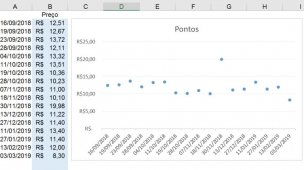
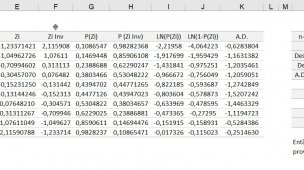
Quando estava realizando o cálculo da ANOVA de apenas um fator, que segue abaixo,
Surgiu uma validação para realizar o cálculo da Diferença Mínima Significativa (DMS), sendo necessário o cálculo do Q-Crítico, Tabela Q que utiliza o Teste de Tukey,
Devido à complexidade do código foi necessário criar várias funções personalizada no MS Excel com programação VBA (Visual Basic Application), segue o exemplo abaixo:

Segue as funções, Qprob (Probabilidade Q), Q-Crítico e uma função intermediária, segue as mesmas abaixo,
1° - Função Intermédiária alnorm
Function alnorm(x As Variant, upper As Variant)
ltone = 7
utzero = 18.66
con = 1.28
a1 = 0.398942280444
a2 = 0.399903438504
a3 = 5.75885480458
a4 = 29.8213557808
a5 = 2.62433121679
a6 = 48.6959930692
a7 = 5.92885724438
b1 = 0.398942280385
b2 = 0.000000038052
b3 = 1.00000615302
b4 = 0.000398064794
b5 = 1.98615381364
b6 = 0.151679116635
b7 = 5.29330324926
b8 = 4.8385912808
b9 = 15.1508972451
b10 = 0.742380924027
b11 = 30.789933034
b12 = 3.99019417011
Dim up As Variant, y As Variant, Z As Variant, retval As Variant
up = upper
Z = x
If (Z < 0) Then
If (up) Then
up = False
Else
up = True
End If
Z = -Z
End If
If ((Z <= ltone) Or (up = True) And (Z <= utzero)) Then
y = 0.5 * Z * Z
If (Z > con) Then
retval = b1 * Exp(-y) / (Z - b2 + b3 / (Z + b4 + b5 / (Z - b6 + b7 / (Z + b8 - b9 / (Z + b10 + b11 / (Z + b12))))))
Else
retval = 0.5 - Z * (a1 - a2 * y / (y + a3 - a4 / (y + a5 + a6 / (y + a7))))
End If
Else
retval = 0
End If
If (up = False) Then
retval = 1 - retval
End If
alnorm = retval
End Function2° - Função da Probabilidade Q
Function Qprob(k As Variant, df As Variant, q As Variant)
Dim vw(1 To 31) As Variant 'Dim vw = new Array(31)
Dim qw(1 To 31) As Variant 'Dim qw = new Array(31)
pcutj = 0.00003
pcutk = 0.0001
step = 0.45
vmax = 1000
cv1 = 0.193064705
cv2 = 0.293525326
cvmax = 0.39894228
Dim cv(0 To 4)
cv(0) = 0
cv(1) = 0.318309886
cv(2) = -0.00268132716
cv(3) = 0.00347222222
cv(4) = 0.0833333333
jmin = 3
jmax = 15
kmin = 7
kmax = 15
Dim retval As Variant, g As Variant, gmid As Variant, r1 As Variant, c As Variant, h As Variant, hj As Variant, v2 As Variant, gstep As Variant, pk As Variant, pk1 As Variant, pk2 As Variant, pj As Variant, j As Variant, jj As Variant, kk As Variant, gk As Variant, w0 As Variant, pz As Variant, x As Variant, jump As Variant, ehj As Variant
retval = 0
g = step * (k ^ -0.2)
gmid = 0.5 * Log(k)
r1 = k - 1
c = Log(k * g * cvmax)
If (c <= vmax) Then
h = step * (df ^ -0.5)
v2 = df * 0.5
If (df = 1) Then
c = cv1
End If
If (df = 2) Then
c = cv2
End If
If (Not ((df = 1) Or (df = 2))) Then
c = Sqr(v2) * cv(1) / (1# + ((cv(2) / v2 + cv(3)) / v2 + cv(4)) / v2)
End If
c = Log(c * k * g * h)
End If
gstep = g
qw(1) = -1
qw(jmax + 1) = -1
pk1 = 1
pk2 = 1
For kk = 1 To kmax
gstep = gstep - g
Do While saida1 = 0
gstep = -gstep
gk = gmid + gstep
pk = 0
If ((pk2 > pcutk) Or (kk <= kmin)) Then
w0 = c - gk * gk * 0.5
pz = alnorm(gk, True)
x = alnorm(gk - q, True) - pz
If (x > 0) Then
pk = Exp(w0 + r1 * Log(x))
If (df <= vmax) Then
jump = -jmax
Do While saida = 0
jump = jump + jmax
For j = 1 To jmax
jj = j + jump
If qw(jj) <= 0 Then
hj = h * j
If (j < jmax) Then
qw(jj + 1) = -1
End If
ehj = Exp(hj)
qw(jj) = q * ehj
vw(jj) = df * (hj + 0.5 - ehj * ehj * 0.5)
End If
pj = 0
x = alnorm(gk - qw(jj), True) - pz
If (x > 0) Then
pj = Exp(w0 + vw(jj) + r1 * Log(x))
End If
pk = pk + pj
If (pj <= pcutj) Then
If ((jj > jmin) Or (kk > kmin)) Then
Exit For
End If
End If
pj = pj
Next
h = -h
If (h > 0) Then saida = 1
Loop
saida = 0
End If
End If
End If
retval = retval + pk
If ((kk > kmin) And (pk <= pcutk) And (pk1 <= pcutk)) Then
Qprob = 1 - retval
End If
pk2 = pk1
pk1 = pk
If (gstep <= 0) Then saida1 = 1
Loop
saida1 = 0
Next
Qprob = 1 - retval
End Function3° - Função Q-Crítico
Function CriticalQ(k As Variant, df As Variant, alpha As Variant)
Delta = 1
cq = 1
Do While (Delta > 0.00001)
p = Qprob(k, df, cq)
If (p < alpha) Then
cq = cq - Delta
Delta = Delta / 2
End If
cq = cq + Delta
Loop
CriticalQ = cq
End FunctionEstes códigos foram adaptados do autor Greg C Elvers.
Com essas funções transcritas, não será mais necessário utilizar os dados da Tabela Q
Com o cálculo de Q-Crítico podemos calcular o DMS que segue abaixo:
=Q-Crítico*Raiz(MS-Within Groups/Máximo(Número itens dos Grupos))
Espero que tenha gostado desse artigo!
Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.
Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.
E ja conhece o meu novo curso online de Excel?
Abraços a todos e até o próximo artigo!
Fabio BALDINI
Frase do Dia: "Se seu experimento precisar de estatísticas, você deveria ter feito um experimento melhor" Autor: Sir Ernest Rutherford