Olá amigos! Sejam bem vindos ao meu novo artigo! Vou apresentar neste artigo uma técnica bastante aplicada da área da Estatística. Esta técnica se chama ANOVA (Analysis of Variance), que significa uma Análise de Variâncias entre Grupos. Vamos ao exemplo, temos três tipos de motores sendo eles classificados como A, B e C. Em cada tipo de motor, retiramos uma amostragem de 5 unidades de cada e fizemos um teste de durabilidade e obtivemos os seguintes resultados, que segue abaixo
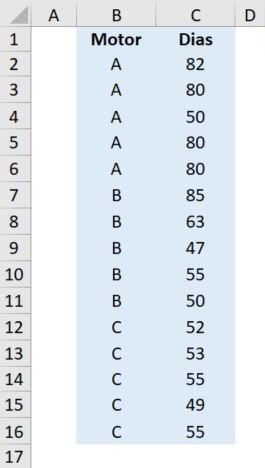
A questão é, podemos com essas amostras aferir que os três motores têm durabilidade igual? Podemos colocar a cotação de compra acreditando que eles teoricamente são iguais? Para responder essa pergunta precisamos utilizar essa técnica para verificar se os motores possuem uma variância próxima, pois se analisarmos somente a média dos grupos ficará muito vago para tomar a decisão. Esta técnica é específica para três ou mais grupos e somente um fator, neste caso será a coluna B - Motor.
Para iniciar os nossos cálculos será necessário mudar o formato dos dados. Vamos transformá-los em tabela. Observe a imagem abaixo.
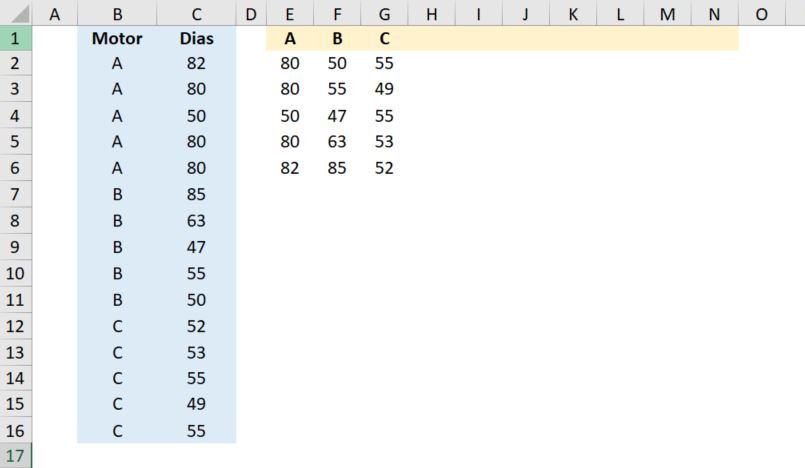
Para trazer os dados que estão nas células E2 até a N30, utilize a fórmula abaixo:
=SE(MAIOR(ÍNDICE(CONT.SE(E$1;$B$2:$B$68)*LIN($B$2:$B$68);0;0);
LIN()-LIN(E$1))=0;"";ÍNDICE($C$1:$C$68;MAIOR(ÍNDICE(
CONT.SE(E$1;$B$2:$B$68)*LIN($B$2:$B$68);0;0);LIN()-LIN(E$1));0))ou em inglês
=IF(LARGE(INDEX(COUNTIF(E$1;$B$2:$B$68)*ROW($B$2:$B$68);0;0);
ROW()-ROW(E$1))=0;"";INDEX($C$1:$C$68;LARGE(INDEX(
COUNTIF(E$1;$B$2:$B$68)*ROW($B$2:$B$68);0;0);ROW()-ROW(E$1));0))Inicialmente teremos que avaliar todos os dados de todo grupo, verificando se os grupos têm diferenças significativas entre eles, e se tiver, qual grupo possui a diferença significativa em comparação a outro grupo. Vamos aos cálculos iniciais,

Número de Variáveis (Célula T1)
=CONT.VALORES(E1:N1)-CONTAR.VAZIO(E1:N1) | =CONT.VALORES(E1:N1)ou em inglês
=COUNTA(E1:N1)-COUNTBLANK(E1:N1) | =COUNTA(E1:N1)SSW (Célula T2) - Sum of Squares Within Groups
=AB3Média Geral (Célula T3)
=MÉDIA(C:C)ou em inglês
=AVERAGE(C:C)TSS (Célula T4) - Total Sum of Squares
=DESVQ(C:C) | =DEVSQ(C:C)SSB ou SS (Célula T5) - Sum of Square Between Groups
=T4-T2MS entre os Grupos (Célula T7)
=T5/(T1-1)MS com os Grupos (Célula T8)
=T2/(CONT.NÚM(E2:N30)-T1)ou em inglês
=T2/(COUNT(E2:N30)-T1)Preparo para o cálculo do teste F - (Célula R10) Numerador
=T1-1Preparo para o cálculo do teste F - (Célula S10) Denominador
=CONT.NÚM(E2:N30)-T1ou em inglês
=COUNT(E2:N30)-T1Preparo para o cálculo do teste F - (Célula T10) X
=T7/T8Cálculo do P-value do Teste F (Célula T11)
=DIST.F.CD(T10;R10;S10)ou em inglês
=F.DIST.RT(T10;R10;S10)Cálculo do F-Crítico (Célula T12)
=INV.F.CD(T13;R10;S10)ou em inglês
=F.INV.RT(T13;R10;S10)Alfa - Margem de aceitação (Célula T3) - 5%
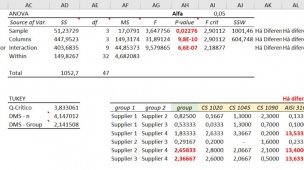
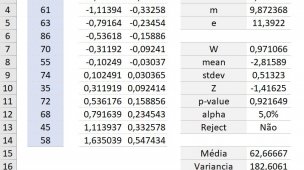
Neste momento o resultado do P-value resultou no valor de 0,03978, como este valor é menor do que o alfa, é necessário aplicar o teste de Tukey (1949), caso o valor seja maior ou igual, podemos afirmar que todos os produtos têm a sua variância muito próxima.
Antes de aplicar o teste de Tukey precisamos dos outros cálculos da tabela demonstrada.
Nome dos Grupos não duplicados - (Célula W5 a W14)
=SE(SEERRO(ÍNDICE($B$2:$B$38;CORRESP(0;ÍNDICE(
CONT.SE($W$4:W4;$B$2:$B$38);0;0);0));"")=0;"";
SEERRO(ÍNDICE($B$2:$B$38;CORRESP(0;ÍNDICE(
CONT.SE($W$4:W4;$B$2:$B$38);0;0);0));""))ou em inglês
=IF(IFERROR(INDEX($B$2:$B$38;MATCH(0;INDEX(
COUNTIF($W$4:W4;$B$2:$B$38);0;0);0));"")=0;"";
IFERROR(INDEX($B$2:$B$38;MATCH(0;INDEX(
COUNTIF($W$4:W4;$B$2:$B$38);0;0);0));""))Contagem de valores de cada Grupo (Célula X5 a X14)
=SE(W5="";"";CONT.SE(B:B;W5))ou em inglês
=IF(W5="";"";COUNTIF(B:B;W5))Soma dos valores de cada Grupo (Célula Y5 a Y14)
=SE(W5="";"";SOMASE(B:B;W5;C:C))ou em inglês
=IF(W5="";"";SUMIF(B:B;W5;C:C))Média dos valores de cada Grupo (Célula Z5 a Z14)
=SE(W5="";"";MÉDIASE(B:B;W5;C:C))ou em inglês
=IF(W5="";"";AVERAGEIF(B:B;W5;C:C))Variância dos valores de cada Grupo (AA5 a AA14)
=SE(W5="";"";VAR.A(DESLOC($A$1;1;CORRESP($W5;$1:$1;0)-1;$X5)))ou em inglês
=IF(W5="";"";VAR.S(OFFSET($A$1;1;MATCH($W5;$1:$1;0)-1;$X5)))Soma Quadrática das Diferenças de cada Grupo - SS (Célula AB5 a AB14)
=SE(W5="";"";DESVQ(DESLOC($A$1;1;CORRESP($W5;$1:$1;0)-1;$X5)))ou em inglês
=IF(W5="";"";DEVSQ(OFFSET($A$1;1;MATCH($W5;$1:$1;0)-1;$X5)))Std Err - Erro Padrão (Célula AC5 a AC14)
=SE(W5="";"";RAIZ($Z$18/Z5))ou em inglês
=IF(W5="";"";SQRT($Z$18/Z5))Lower - Intervalo Inferior (Célula AD5 a AD14)
=SE(W5="";"";X25-AC5*INV.T.BC($T$13;$Y$18))ou em inglês
=IF(W5="";"";X25-AC5*T.INV.2T($T$13;$Y$18))Upper - Intervalo Superior (Célula AE5 a AE14)
=SE(W5="";"";X25+AC5*INV.T.BC($T$13;$Y$18))ou em inglês
=IF(W5="";"";X25+AC5*T.INV.2T($T$13;$Y$18))Definido as informações individuais de cada grupo, precisamos dos restantes das informações. Segue abaixo
Variações "Entre os Grupos"
SS - (Célula X17) | =T5
df - (Célula Y17) | =R10
MS - (Célula Z17) | =T7
F - Célula (Célula AA17) | =T10
P-value (Célula AB17) | =T11
F Crítico (Célula AC17) | =T12
Omega Sq (Célula AE17) | =(X20-Y20*Z18)/(X20+Z18)
RMSSE (Célula AD17)
=RAIZ(DESVQ(DESLOC($Z$4;1;0;N;1))/(Z18*Y17))ou em inglês
=SQRT(DEVSQ(OFFSET($Z$4;1;0;N;1))/(Z18*Y17))Variações "Com os Grupos"
SS - (Célula X18) | =T2
df - (Célula Y18) | =S10
MS - (Célula Z18) | =T8
Demonstrado todas as fórmulas e analisando o P-value do ANOVA, vamos aplicar o teste de Tukey onde precisaremos da Tabela Q - Tabela com amplitude total estudentizada.

Não será demonstrado o cálculo do Q-Crítico (Valor da amplitude total estudentizada), pois devido a sua complexidade, tanto de cálculo quanto de entendimento, será abordado em outro artigo, onde a resposta se encontra na célula AB29, para realizar este cálculo serão necessárias 3 informações, segue abaixo
n - Número de grupos - Célula T1 | 3
df - Graus de Liberdade - Célula Y18 | 12
Alfa - Margem de Aceitação - Célula T13 | 5%
Neste exemplo o valor do Q-Crítico resultou o valor de 3,77481842041015.
Com o Q-Crítico será necessário fazer as combinações entre os grupos para verificar qual grupo tem a diferença em comparação a outros grupos. Vamos aos cálculos.
Mean - Diferença entre as Médias dos Grupos (Célula Y34 a Y40)
=SE($V34="";"";ÍNDICE($X$25:$X$28;CORRESP(
W34;$W$25:$W$28;0);0)-ÍNDICE($X$25:$X$28;
CORRESP(X34;$W$25:$W$28;0);0))ou em inglês
=IF($V34="";"";INDEX($X$25:$X$28;MATCH(
W34;$W$25:$W$28;0);0)-INDEX($X$25:$X$28;
MATCH(X34;$W$25:$W$28;0);0))Std Error - Erro entre os Grupos (Célula Z34 a Z40)
=SE($V34="";"";RAIZ($Z$29/$AA$29/MÉDIA.HARMÔNICA(
ÍNDICE($Y$25:$Y$28;CORRESP(W34;$W$25:$W$28;0);0);
ÍNDICE($Y$25:$Y$28;CORRESP(X34;$W$25:$W$28;0);0))))ou em inglês
=IF($V34="";"";SQRT($Z$29/$AA$29/HARMEAN(
INDEX($Y$25:$Y$28;MATCH(W34;$W$25:$W$28;0);0);
INDEX($Y$25:$Y$28;MATCH(X34;$W$25:$W$28;0);0))))Q-stat - (Célula AA34 a AA40)
=SE($V34="";"";Y34/Z34)ou em inglês
=IF($V34="";"";Y34/Z34)Lower (Célula AB34 a AB40)
=SE($V34="";"";Y34-Z34*AB$29)ou em inglês
=IF($V34="";"";Y34-Z34*AB$29)Upper (Célula AC34 a AC40)
=SE($V34="";"";Y34+Z34*AB$29)ou em inglês
=IF($V34="";"";Y34+Z34*AB$29)P-value (Célula AD34 a AD40)
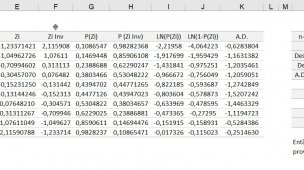
Este item também será abordado em outro artigo devido sua alta complexidade mas, para calcular serão necessários três valores.
São eles:
n- Quantidade de grupos | 3
df - Graus de Liberdade | 12
q-stat - Valor calculado na célula AA34 a AA30 | 2,70528893748785
Neste primeiro exemplo teremos o resultado de 0,177475756934104. Devemos fazer este cálculo para todas as combinações entre os grupos.
Mean-Crit (Célula AE34 a AE40)
=SE($V34="";"";Z34*AB$29)ou em inglês
=IF($V34="";"";Z34*AB$29)Cohen d (Célula AF34 a AF40)
=SE($V34="";"";Y34*RAIZ(AA$29/Z$29))ou em inglês
=IF($V34="";"";Y34*SQRT(AA$29/Z$29))Para verificar qual Grupo tem diferença em relação aos outros grupos, é possível realizar dois tipos de verificação, vamos aos dois cálculos
1° Cálculo - Verificação da Diferença pelo Alfa (Célula AG34 a AG40)
=SE(W34="";"";SE(AD34<=$T$13;"Diferente";""))ou em inglês
=IF(W34="";"";IF(AD34<=$T$13;"Diferente";""))2° Cálculo - Verificação pela DMS - Diferença Mínima Significativa (Células AH34 a AH40)
Segue o cálculo da DMS que está na célula AH32
=AB29*RAIZ(Z18/MÁXIMO(X5:X13))ou em inglês
=AB29*SQRT(Z18/MAX(X5:X13))Com o valor do DMS é só verificar qual média é maior do que este valor, segue a fórmula abaixo
=SE(V34="";"";SE(ABS(Y34)>$AH$32;"Diferença";""))ou em inglês
=IF(V34="";"";IF(ABS(Y34)>$AH$32;"Diferença";""))Neste caso podemos afirmar que existe uma diferença significativa entre o Motor A e C, devido aos seus parâmetros iniciais, portanto se fizer uma compra dos três motores acreditando que são iguais para avaliar somente o preço, deverá retirar o Motor C desta análise.
Espero que tenha gostado desse artigo!
Caso tenha alguma sugestão de outra técnica, poste aqui nos comentários.
Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do Excel.
E ja conhece o meu novo curso online de Excel?
Abraços a todos e até o próximo artigo!
Fabio BALDINI
Frase do Dia: "A imaginação é mais importante do que o conhecimento. O conhecimento é limitado. A imaginação envolve o mundo." Autor: Albert Einstein
OBS: Quero agradecer imensamente ao Grande Mestre e Amigão Alessandro Trovato pelas eternas revisões dos artigo para que sempre fique esmero. Obrigadão grande Mestre!




Link permanente