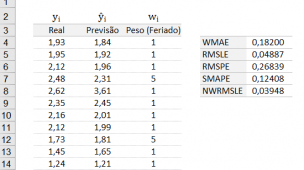
Olá pessoal! Bem vindo ao meu novo artigo! Estava fazendo uma disciplina de Análises Multivariadas com o Prof. Dr. Bruno Grimaldo Martinho Churata, e o professor falou em umas das suas aulas sobre a Distância de Mahalanobis, mais conhecida como a Distância Estatística, demonstrado pelo matemático indiano Prasanta Chandra Mahalanobis em 1936.
Essa distância tem se tornado um dos coeficientes padrões para o caso em que todas as variáveis envolvidas são quantitativas (ver Kotz e Johnson, 1985).
Estudando e analisando a mesma, vi que ela poderá ser analisada em três aplicações vamos a elas:
1° Aplicação - A distância entre grupos com a inserção de uma nova variável
Quando a matriz de covariância será na diagonal, onde a distância de Mahalanobis será a distância Euclidiana normalizada.

Nesta aplicação, a distância é muito utilizado para aprendizagem automática e visão computacional, pois quando se tem os dois conjuntos de valores, e precisamos inserir mais um valor, para qual grupo o novo valor irá pertencer? Para o Grupo 1 ou o Grupo 2? Se utilzarmos a distância Euclidiana o valor irá escolher os dois grupos, dificultando a escolha, mas quando utilizamos a Distância de Mahalanobis é possível verificar que o novo valor irá pertencer ao Grupo 1, onde este novo ponto estará mais próximo. O interessante deste método é que quando um grupo contendo amostras esparçadas o valor da distância será menor, onde ao contrário é válido, um grupo de amostras mais próximas o valor da distância será maior. Esta distância, além de ponderar pelo inverso dos desvios padrões de cada uma das variáveis, também leva em conta o grau de inter-relação que existe entre elas (ver Bolshev, 1969).
Resumindo, quando os dados de um grupo são mais esparsados, a variabilidade é maior e o peso tende a diminuir, uma vez que é ponderado pelo inverso da mesma.
Vamos as fórmulas:
Célula F3 - Distância de Mahalanobis para a Variável 1 em relação ao valor da Célula F2
=RAIZ((F2-MÉDIA(A:A))^2/DESVPAD(A:A)^2)ou em inglês
=SQRT((F2-AVERAGE(A:A))^2/STDEV(A:A)^2)Célula G3 - Distância de Mahalanobis para a Variável 2 em relação ao valor da Célula F2
=RAIZ((F2-MÉDIA(C:C))^2/(DESVPAD(C:C)^2))ou em inglês
=SQRT((F2-AVERAGE(C:C))^2/(STDEV(C:C)^2))Célula F4 - Distância Euclidiana para a Variável 1 em relação ao valor da Célula F2
=RAIZ(($F$2-MÉDIA(A:A))^2)ou em inglês
=SQRT(($F$2-AVERAGE(A:A))^2)Célula G4 - Distância Euclidiana para a Variável 2 em relação ao valor da Célula F2
=RAIZ(($F$2-MÉDIA(C:C))^2)ou em inglês
=SQRT(($F$2-AVERAGE(C:C))^2)Célula F6 - Média da Variável 1
=MÉDIA(A:A)ou em inglês
=AVERAGE(A:A)Célula G6 - Média da Variável 2
=MÉDIA(C:C)ou em inglês
=AVERAGE(C:C)Nas células F11 a G12 é somar os valores com a média e F15 a G16 somente diminuir os valores com as médias
2° Aplicação - Quando é necessário calcular a distância entre dois grupos com duas variáveis, independentes.
Nesta aplicação entre dois vetores da mesma distribuição será calculado a matriz de covariância.

Onde podemos afirmar que quanto maior for o valor desta distância, maior será o número de desvios padrões que um elemento/grupo está distante do centro de outro grupo e consequemente menor a sua chance de ser um elemento do mesmo grupo.
Vamos as fórmulas:
Matriz C^t
Célula G4
=(VAR.P(B:B)*CONT.NÚM(A:A)+VAR.P(E:E)*CONT.NÚM(D:D))/(CONT.NÚM(A:A)+CONT.NÚM(D:D)-$H$1)ou inglês
=(VAR.P(B:B)*COUNT(A:A)+VAR.P(E:E)*COUNT(D:D))/(COUNT(A:A)+COUNT(D:D)-$H$1)Célula H4
=-(COVARIAÇÃO.P(A:A;B:B)*CONT.NÚM(A:A)+COVARIAÇÃO.P(D:D;E:E)*CONT.NÚM(D:D))/(CONT.NÚM(A:A)+CONT.NÚM(D:D)-$H$1)ou inglês
=-(COVARIANCE.P(A:A;B:B)*COUNT(A:A)+COVARIANCE.P(D:D;E:E)*COUNT(D:D))/(COUNT(A:A)+COUNT(D:D)-$H$1)Célula G5
=-(COVARIAÇÃO.P(A:A;B:B)*CONT.NÚM(A:A)+COVARIAÇÃO.P(D:D;E:E)*CONT.NÚM(D:D))/(CONT.NÚM(A:A)+CONT.NÚM(D:D)-$H$1)ou inglês
=-(COVARIANCE.P(A:A;B:B)*COUNT(A:A)+COVARIANCE.P(D:D;E:E)*COUNT(D:D))/(COUNT(A:A)+COUNT(D:D)-$H$1)Célula H5
=(VAR.P(A:A)*CONT.NÚM(A:A)+VAR.P(D:D)*CONT.NÚM(D:D))/(CONT.NÚM(A:A)+CONT.NÚM(D:D)-$H$1)ou inglês
=(VAR.P(A:A)*COUNT(A:A)+VAR.P(D:D)*COUNT(D:D))/(COUNT(A:A)+COUNT(D:D)-$H$1)Célula H7 - Determinante
=MATRIZ.DETERM(G4:H5)ou inglês
=MDETERM(G4:H5)Matriz Inversa
Célula G10
=G4/$H$7Célula H10
=H4/$H$7Célula G11
=G5/$H$7Célula H11
=H5/$H$7Célula H13 - Distância de Mahalanobis - D²
=MATRIZ.MULT(MATRIZ.MULT(ESCOLHER({1\2};MÉDIA(A:A)-MÉDIA(D:D);MÉDIA(B:B)-MÉDIA(E:E));G10:H11);ESCOLHER({1;2};MÉDIA(A:A)-MÉDIA(D:D);MÉDIA(B:B)-MÉDIA(E:E)))ou em inglês
=MMULT(MMULT(CHOOSE({1\2};AVERAGE(A:A)-AVERAGE(D:D);AVERAGE(B:B)-AVERAGE(E:E));G10:H11);CHOOSE({1;2};AVERAGE(A:A)-AVERAGE(D:D);AVERAGE(B:B)-AVERAGE(E:E)))Célula H15 - Distância de Mahalanobis - D
=RAIZ(H13)ou em inglês
=SQRT(H13)3° Aplicação - Extensão da Distância de Mahalanobis, Balakrishnan e Sangghvi (1968) e Kurczynski (1970)

Desta aplicação irá resultar a distância de cada conjunto referente ao seu centro de todo o conjunto. A Distância Métrica de Mahalanobis é dita invariante com relação a escala. ou seja, ela dá a mesma distância para qualquer que seja a unidade usada para medir as variáveis.
Antes de demonstrar o cálculo final, para essa aplicação precisaremos de 4 tabelas auxiliares são elas: Matriz dos pontos em relação com a média, Matriz de Variância e Covariância e a Matriz Inversa
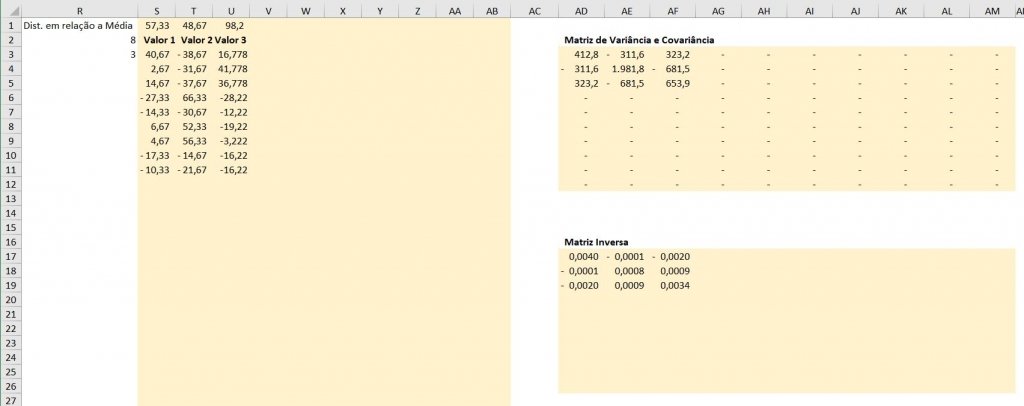
Célula R2
=CONT.NÚM(A:A)-1ou em inglês
=COUNT(A:A)-1Célula R3
=CONT.SE(A3:J3;">0")ou em inglês
=COUNTIF(A3:J3;">0")Célula S1 a AB1
=SEERRO(MÉDIA(A:A);"")ou em inglês
=IFERROR(AVERAGE(A:A);"")Célula S2 a AB2
=SE(A2=0;"";A2)ou em inglês
=IF(A2=0;"";A2)Célula S3 a AB200
=SE(A3="";"";A3-S$1)ou em inglês
=IF(A3="";"";A3-S$1)Célula AD3 a AM12
=SOMARPRODUTO(DESLOC($S$3;0;ÍNDICE((LIN()-LIN($AD$3));1;1);$R$2+1;1);DESLOC($S$3;0;ÍNDICE(COL()-COL($AD$3);1;1);$R$2+1;1))/$R$2ou em inglês
=SUMPRODUCT(OFFSET($S$3;0;INDEX((ROW()-ROW($AD$3));1;1);$R$2+1;1);OFFSET($S$3;0;INDEX(COLUMN()-COLUMN($AD$3);1;1);$R$2+1;1))/$R$2Célula AD17 a AM26
=SEERRO(ÍNDICE(MATRIZ.INVERSO(DESLOC($AD$3;0;0;$R$3;$R$3));LIN()-LIN($AD$17)+1;COL()-COL($AD$17)+1);"")ou em inglês
=IFERROR(INDEX(MINVERSE(OFFSET($AD$3;0;0;$R$3;$R$3));ROW()-ROW($AD$17)+1;COLUMN()-COLUMN($AD$17)+1);"")Matriz Final
Célula AO3 a AX200
=SEERRO(MATRIZ.MULT(DESLOC($S3;0;0;1;$R$3);DESLOC(AD$17;0;0;$R$3;1));"")ou em inglês
=IFERROR(MMULT(OFFSET($S3;0;0;1;$R$3);OFFSET(AD$17;0;0;$R$3;1));"")Agora com as matrizes criadas podemos demonstras as fórmulas finais para a Distância de Mahalanobis Extendida.

Célula L3 a L200 - D Mahalanobis
=SE(S3="";"";RAIS(SOMARPRODUTO(AO3:AX3;S3:AB3)))ou em inglês
=IF(S3="";"";SQRT(SUMPRODUCT(AO3:AX3;S3:AB3)))Célula M3 a M200 - D² Mahalanobis
=SEERRO(L3^2;"")ou em inglês
=IFERROR(L3^2;"")Célula N3 a N200 - Critical Value
=SE(M3="";"";INV.QUIQUA(1-$N$1;LINS($N$3:N3)))ou em inglês
=IF(M3="";"";CHISQ.INV(1-$N$1;ROWS($N$3:N3)))Célula O3 a O200 - Probability
=SE(M3="";"";1-DIST.QUIQUA(N3;LINS($O$3:O3);1))ou em inglês
=IF(M3="";"";1-CHISQ.DIST(N3;ROWS($O$3:O3);1))Célula P3 a P200 - Probabilidade da Distância de Mahalanobis
=SE(M3="";"";1-DIST.QUIQUA(M3;$R$3;1))ou em inglês
=IF(M3="";"";1-CHISQ.DIST(M3;$R$3;1))Gostaria de agradecer novamente ao Prof. Dr. Bruno Grimaldo Martinho Churata pelos seus ensinamentos em suas disciplinas. Muito obrigado Professor.
Espero que tenham gostado desse artigo! Caso tenha alguma sugestão de melhorias, poste aqui nos comentários.
Se gostou, curta e compartilhem para que todos saibam o que é possível fazer dentro do Excel.
E ja conhece o meu novo curso online de Excel?
Abraços a todos e até o próximo artigo!
Fabio BALDINI
Frase do dia: "Não há problema em assumir riscos. Não há problema em fracassar. Se você não está ultrapassando seus limites, não está crescendo tanto quanto poderia" Autor: Stacey Cunningham