▷ Teste Diebold-Mariano – Comparação entre duas Previsões no Excel

Olá seja bem vindo ao meu mais novo artigo!

Neste artigo será demonstrado como construir passo a passo o Teste Estatístico de Diebold-Mariano, realizando uma comparação entre as previsões, demonstrando se as mesmas possuem alguma diferença significativa, vamos ao exemplo abaixo

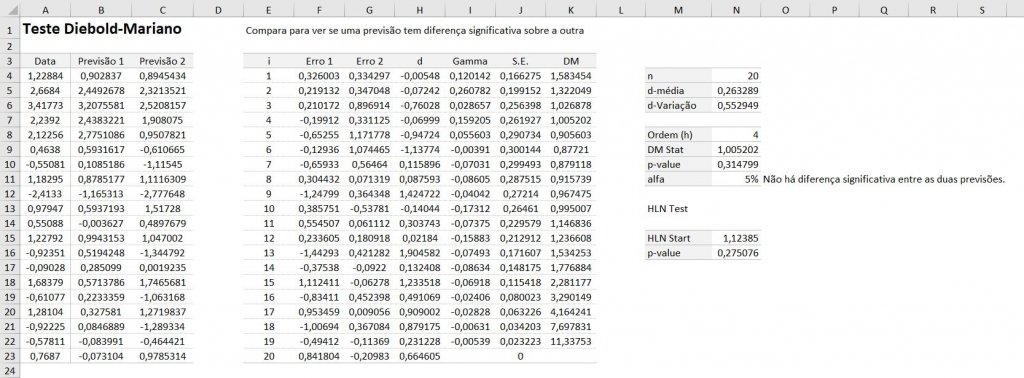
Segue os dados para validar as fórmulas

Data	Previsão 1	Previsão 2
1,22884	0,902837	0,8945434
2,6684	2,4492678	2,3213521
3,41773	3,2075581	2,5208157
2,2392	2,4383221	1,908075
2,12256	2,7751086	0,9507821
0,4638	0,5931617	-0,610665
-0,55081	0,1085186	-1,11545
1,18295	0,8785177	1,1116309
-2,4133	-1,165313	-2,777648
0,97947	0,5937193	1,51728
0,55088	-0,003627	0,4897679
1,22792	0,9943153	1,047002
-0,92351	0,5194248	-1,344792
-0,09028	0,285099	0,0019235
1,68379	0,5713786	1,7465681
-0,61077	0,2233359	-1,063168
1,28104	0,327581	1,2719837
-0,92225	0,0846889	-1,289334
-0,57811	-0,083991	-0,464421
0,7687	-0,073104	0,9785314

Vamos para as colunas de cálculos

1° Passo - Calcular o Erro 1 (em comparação ao dado) | Coluna F

=A4-B4

2° Passo - Calcular o Erro 2 (em comparação ao dado) | Coluna G

=A4-C4

3° Passo - Calcular a distância entre os erros | Coluna H

=F4^2-G4^2

4° Passo - Calcular o Gamma | Coluna I

=SEERRO(SOMA(ÍNDICE((H5:H$23-$N$5)*(DESLOC($H$4:$H$23;0;0;N$4-LINS($I$4:I4))-$N$5);0))/N$4;"")

ou em inglês

=IFERROR(SUM(INDEX((H5:H$23-$N$5)*(OFFSET($H$4:$H$23;0;0;N$4-ROWS($I$4:I4))-$N$5);0))/N$4;"")

5° Passo - Calcular o S.E. | Coluna J

=RAIZ(N6/N4)

ou em inglês

=SQRT(N6/N4)

6° Passo - Calcular o DM | Coluna K

=SEERRO($N$5/J4;"")

ou em inglês

=IFERROR($N$5/J4;"")

Após os cálculos dos índices

n-número de Amostras | N4

=CONT.NÚM(A4:A23)

ou em inglês

=COUNT(A4:A23)

d-média | N5

=MÉDIA(H4:H23)

ou em inglês

=AVERAGE(H4:H23)

d-variação | N6

=VAR.P(H4:H23)

Ordem (h) | N8

=ARRED(N4^(1/3)+1;0)

ou em inglês

=ROUND(N4^(1/3)+1;0)

DM Stat | N9

=ÍNDICE($K$4:$K$23;$N$8)

ou em inglês

=INDEX($K$4:$K$23;$N$8)

p-value | N10

=2*(1-DIST.NORMP.N(ÍNDICE($K$4:$K$23;$N$8);1))

ou em inglês

=2*(1-NORM.S.DIST(INDEX($K$4:$K$23;$N$8);1))

HLN Start| N15

=ÍNDICE($K$4:$K$23;$N$8)*RAIZ((N4+1-2*N8+N8*(N8-1))/N4)

ou em inglês

=INDEX($K$4:$K$23;$N$8)*SQRT((N4+1-2*N8+N8*(N8-1))/N4)

p-value HLN Teste | N16

=DIST.T.BC(N15;N4-1)

ou em inglês

=T.DIST.2T(N15;N4-1)

Caso o p-value da célula N10 for menor do que 5% (que foi estipulado) haverá diferença significativa entre as previsões, mas neste exemplo foi acima, portanto podemos afirmar que não há diferença significativa entre as previsões.

Espero que tenha gostado desse artigo !

Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.

Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.

E ja conhece o meu novo curso online de Excel?

Abraços a todos e até o próximo artigo!

Fabio BALDINI

Frase do Dia: "É melhor caminhar sozinho do que caminhar com uma multidão que está indo na direção errada" Autor: Herman Siu