▷ Correlação de Spearman no Excel

Olá seja bem vindo ao meu mais novo artigo

A Correlação de Spearman avalia a relação monotônica entre duas variáveis contínuas ou ordinais, seja ela linear ou não.

Em uma relação monotônica, as variáveis tendem a mudar juntas, mas não necessariamente a uma taxa constante. O coeficiente de Correlação de Spearman baseia-se nos valores classificados (utilizando o Raking de Besson) de cada variável, em vez de os dados brutos. Ou seja, caso não seja observada uma relação linear entre as variáveis, o coeficiente de Spearman é uma ótima alternativa.

Lembrando que a análise de correlação pelo coeficiente de Pearson e Spearman é inviabilizada caso os dados não sigam uma distribuição normal.

Mas vamos ao exemplo e aos cálculos no Excel.

Correlação de Spearman no Excel

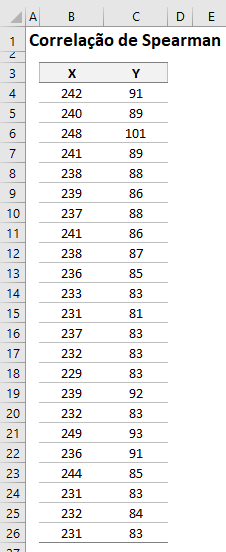
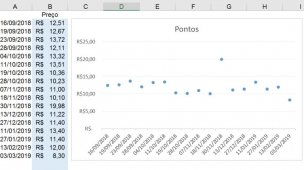
Antes de iniciar os cálculos é necessário criar duas colunas auxiliares utilizando a fórmula do Ranking de Besson para visualizar dos dados no Gráfico de Dispersão no Excel.

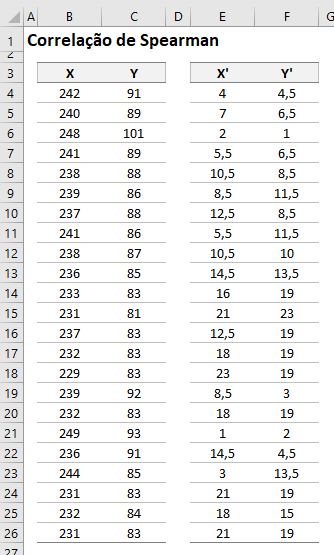
Segue a fórmula do Ranking de Besson no Excel para a variável X, que no Excel já tem nativo, segue na celula E4

=ORDEM.MÉD(B4;B$4:B$26;0)

ou em inglês

=RANK.AVG(B4;B$4:B$26;0)

Segue a fórmula do Ranking de Besson no Excel para a variável Y, que no Excel já tem nativo, segue na celula E4

=ORDEM.MÉD(C4;C$4:C$26;0)

ou em inglês

=RANK.AVG(C4;C$4:C$26;0)

Com as duas colunas criadas é possível realizar o gráfico de dispersão para visualizar a Correlação de Spearman

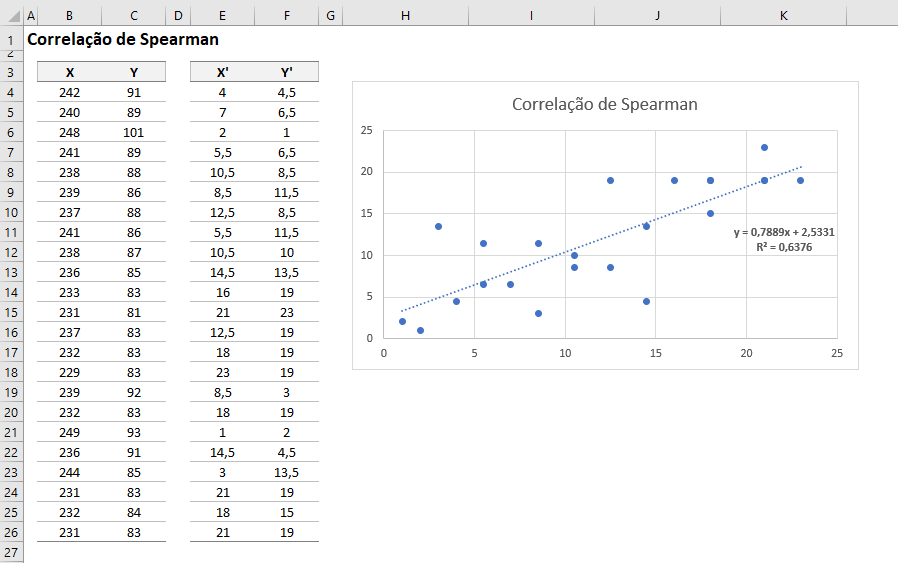
Correlação de Spearman Dinâmico no Excel

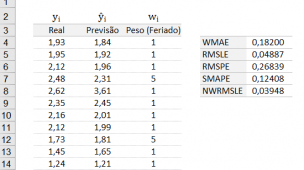
Será demonstrado os cálculos para a obteção dos valores da correlação de Spearman dinâmico, que segue abaixo

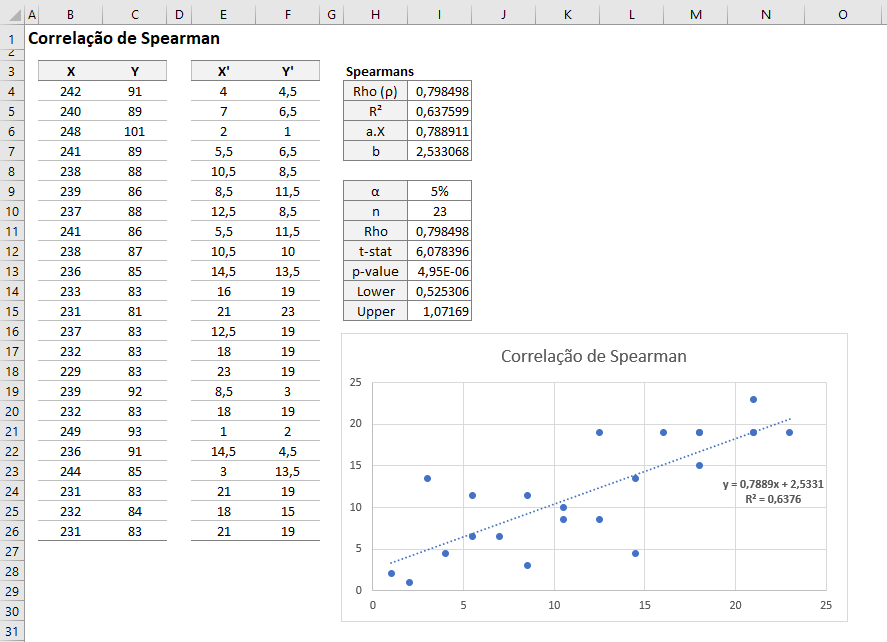
Vamos as fórmulas!

Segue a Correlação de Spearman, que segue na célula I4

=CORREL(ORDEM.MÉD(B4:B26;B$4:B$26;0);ORDEM.MÉD(C4:C26;C$4:C$26;0))

ou em inglês

=CORREL(RANK.AVG(B4:B26;B$4:B$26;0);RANK.AVG(C4:C26;C$4:C$26;0))

Segue o R² da Correlação de Spearman, que segue na célula I5

=CORREL(ORDEM.MÉD(B4:B26;B$4:B$26;0);ORDEM.MÉD(C4:C26;C$4:C$26;0))^2

ou em inglês

=CORREL(RANK.AVG(B4:B26;B$4:B$26;0);RANK.AVG(C4:C26;C$4:C$26;0))^2

Para calcular o valor de a.X, segue a fórmula na célula I6

=INCLINAÇÃO(ORDEM.MÉD(C4:C26;C$4:C$26;0);ORDEM.MÉD(B4:B26;B$4:B$26;0))

ou em inglês

=SLOPE(RANK.AVG(C4:C26;C$4:C$26;0);RANK.AVG(B4:B26;B$4:B$26;0))

Para calcular o valor de b, segue a fórmula na célula I7

=INTERCEPÇÃO(ORDEM.MÉD(C4:C26;C$4:C$26;0);ORDEM.MÉD(B4:B26;B$4:B$26;0))

ou em inglês

=INTERCEPT(RANK.AVG(C4:C26;C$4:C$26;0);RANK.AVG(B4:B26;B$4:B$26;0))

Para a contagem de número de amostras n, segue a fórmula na celula I10

=CONT.NÚM(B4:B26)

ou em inglês

=COUNT(B4:B26)

Para o t-stat, segue a fórmula na célula I12

=I4/RAIZ((1-I4^2)/(I10-2))

ou em inglês

=I4/SQRT((1-I4^2)/(I10-2))

O cálculo do p-value, segue a fórmula na célula I13

=1-DIST.BETA((ABS(I12)^2*1/(I10-2))/(1+ABS(I12)^2*1/(I10-2));1/2;(I10-2)/2;1)

ou em inglês

=1-BETA.DIST((ABS(I12)^2*1/(I10-2))/(1+ABS(I12)^2*1/(I10-2));1/2;(I10-2)/2;1)

Para o Lower, segue a fórmula na célula I14

=I4-RAIZ((1-I4^2)/(I10-2))*RAIZ(INV.BETA(1-I9;1/2;(I10-2)/2)*(I10-2)/(1*(1-INV.BETA(1-I9;1/2;(I10-2)/2))))

ou em inglês

=I4-SQRT((1-I4^2)/(I10-2))*SQRT(BETA.INV(1-I9;1/2;(I10-2)/2)*(I10-2)/(1*(1-BETA.INV(1-I9;1/2;(I10-2)/2))))

Para o Upper, segue a fórmula na célula I15

=I4+RAIZ((1-I4^2)/(I10-2))*RAIZ(INV.BETA(1-I9;1/2;(I10-2)/2)*(I10-2)/(1*(1-INV.BETA(1-I9;1/2;(I10-2)/2))))

ou em inglês

=I4+SQRT((1-I4^2)/(I10-2))*SQRT(BETA.INV(1-I9;1/2;(I10-2)/2)*(I10-2)/(1*(1-BETA.INV(1-I9;1/2;(I10-2)/2))))

Segue a Correlação de Spearman Dinâmica e em relação a Correlação de Pearson

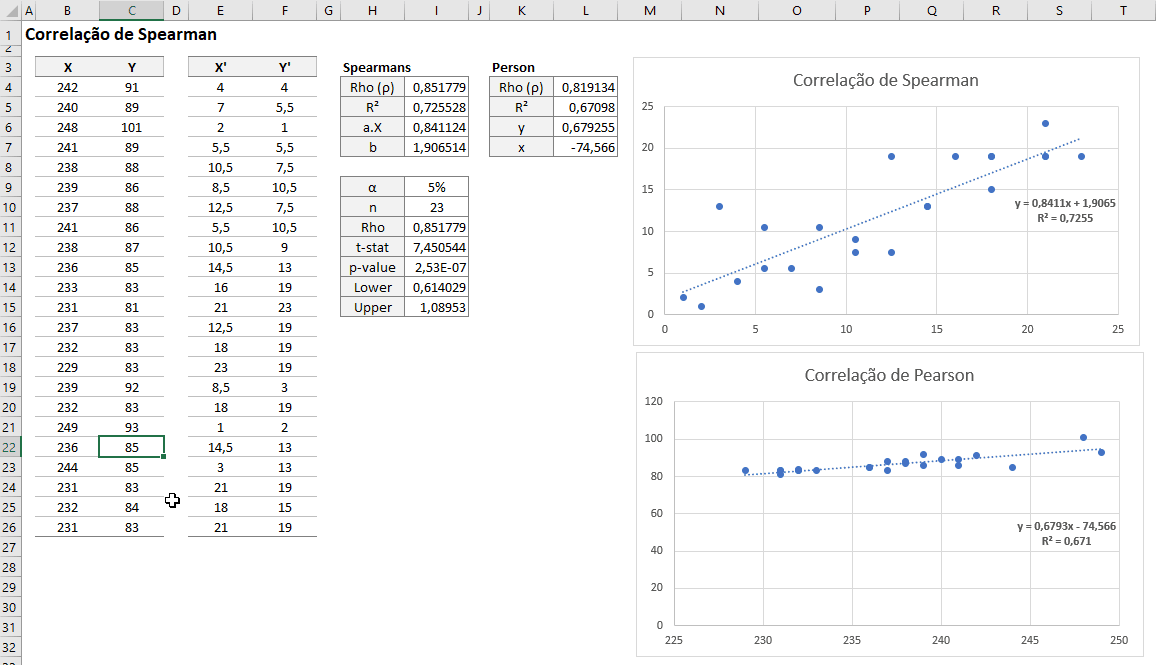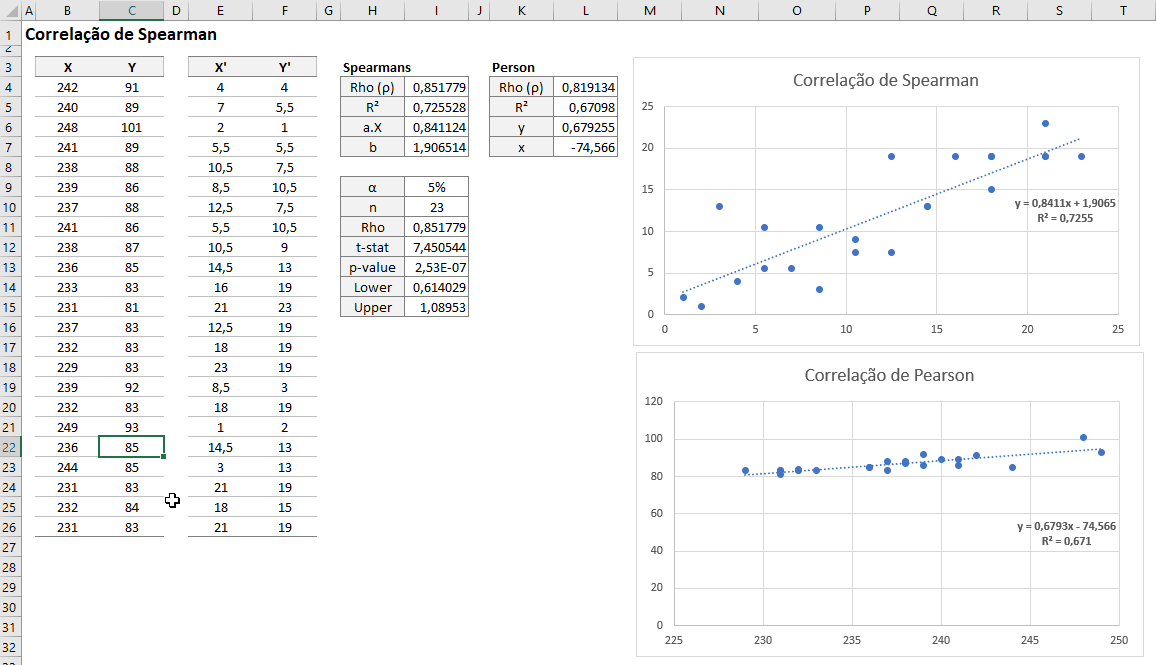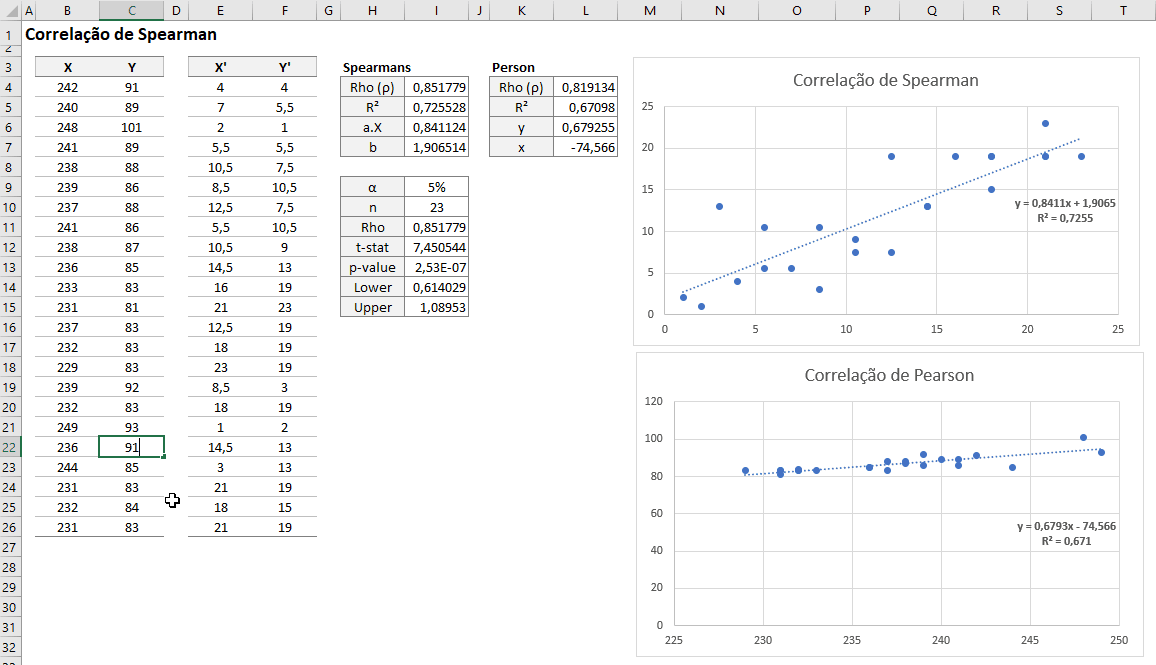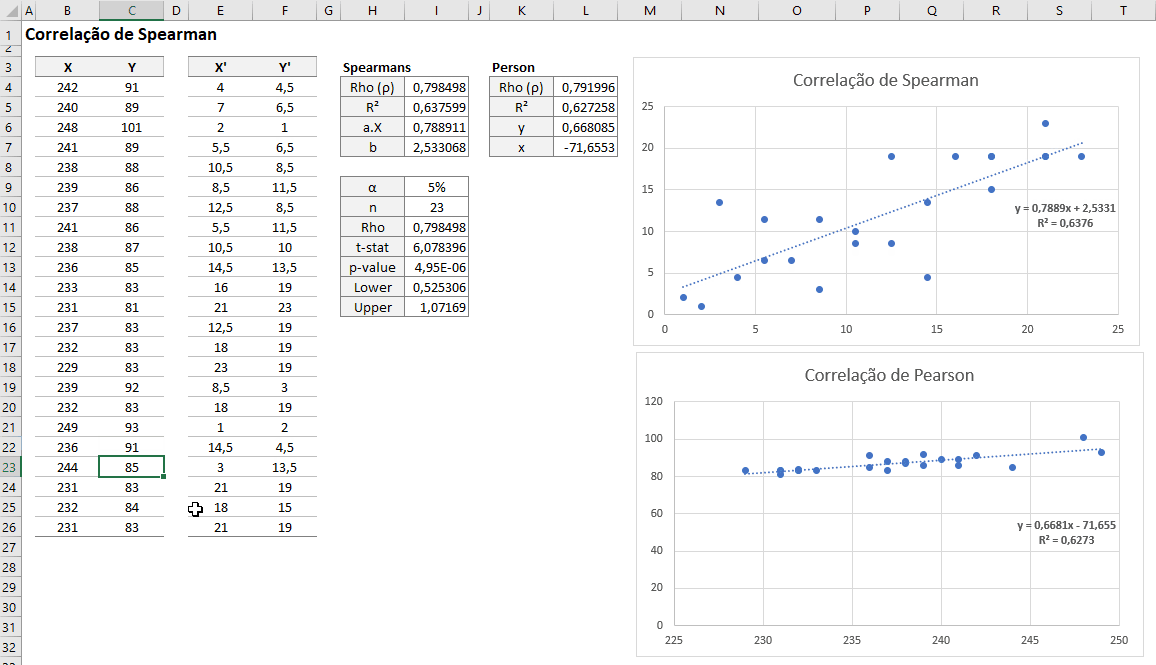
Espero que tenha gostado desse artigo!

Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.

Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.

Venha fazer o melhor curso EAD de Excel comigo! Clique e compare!

Abraços a todos e até o próximo artigo!

Fabio BALDINI

Frase do Dia: "Só se aprende com a experiência. Portanto, não importa o que as pessoas lhe digam, você tem que viver e cometer seus próprios erros para aprender." Autor: Emma Watson