▷ Teste de Normalidade Shapiro-Wilk no Excel

Olá seja bem vindo ao meu novo artigo

O teste de Shapiro-Wilk é um teste de normalidade não paramétrico. Foi publicado em 1965 por Samuel Sanford Shapiro e Martin Wilk. O objetivo deste teste é fornecer uma estatística de teste para avaliar se uma amostra tem distribuição Normal. O teste pode ser utilizado para amostras de qualquer tamanho (recomenda-se até 5.000 amostras).

Segue abaixo o link do artigo original publicado em 1965

https://www.jstor.org/stable/2333709

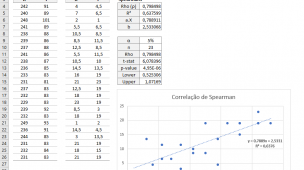
Analisando os dados exemplo abaixo:

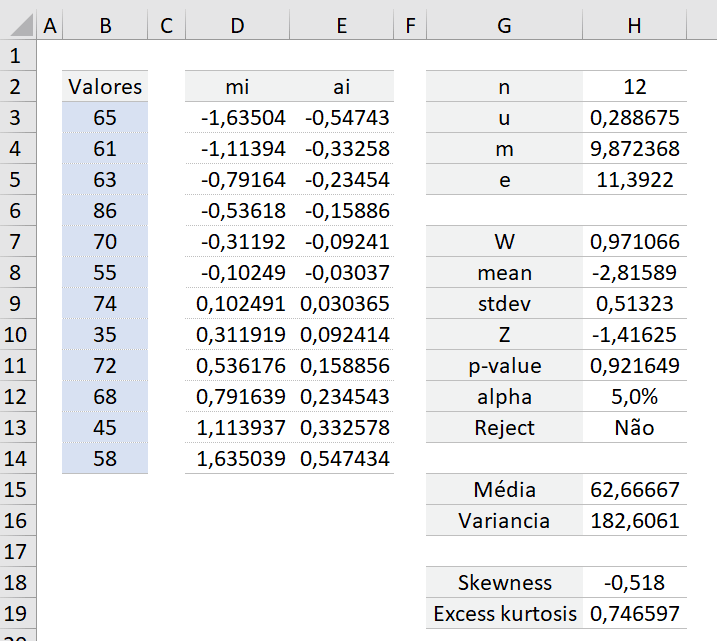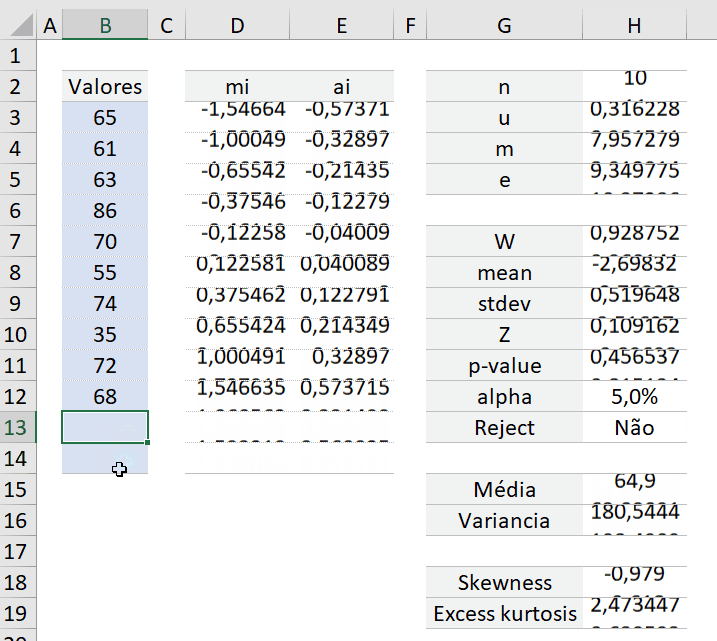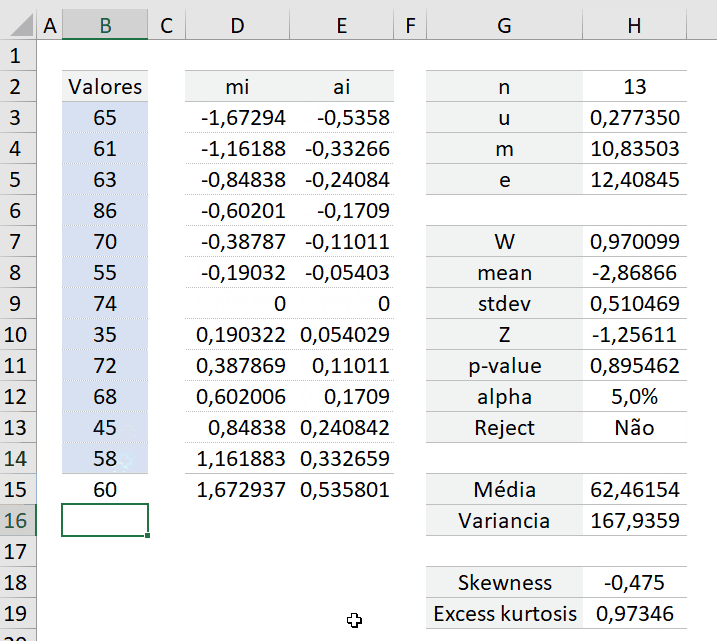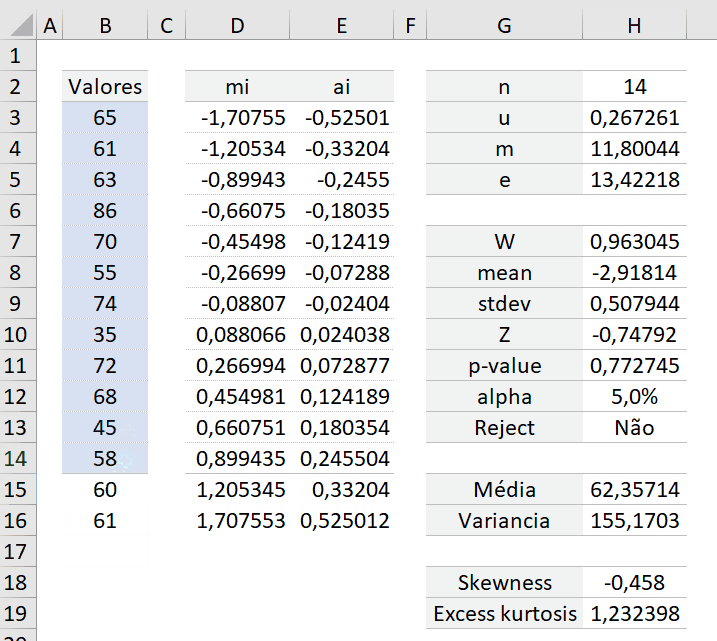
Vamos as fórmulas:

Coluna Auxiliar mi | Coluna D

=SE(B3="";"";INV.NORMP((LINS($D$3:D3)-0,375)/($H$2+0,25)))

ou em inglês

=IF(B3="";"";NORMSINV((ROWS($D$3:D3)-0,375)/($H$2+0,25)))

Coluna Auxiliar ai | Coluna E

=SE(B3="";"";SE(LINS($E$3:E3)=$H$2; -2,70605*$H$3^5+4,434685*$H$3^4 -2,07119*$H$3^3-0,147981*$H$3^2 +0,221157*$H$3 +D3/RAIZ($H$4); SE(LINS($E$3:E3)+1=$H$2; -3,582633*$H$3^5+5,682633*$H$3^4 -1,752461*$H$3^3 -0,293762*$H$3^2 +0,042981*$H$3 +D3/RAIZ($H$4);SE(LINS($E$3:E3)=2;-DESLOC($E$2;$H$2-1;0);SE(LINS($E$3:E3)=1;-DESLOC($E$2;$H$2;0);D3/RAIZ($H$5))))))

ou em inglês

=IF(B3="";"";IF(ROWS($E$3:E3)=$H$2;-2,70605*$H$3^5 +4,434685*$H$3^4 -2,07119*$H$3^3-0,147981*$H$3^2 +0,221157*$H$3 +D3/SQRT($H$4); IF(ROWS($E$3:E3)+1=$H$2; -3,582633*$H$3^5 +5,682633*$H$3^4 -1,752461*$H$3^3 -0,293762*$H$3^2 +0,042981*$H$3 +D3/SQRT($H$4);IF(ROWS($E$3:E3)=2; -OFFSET($E$2;$H$2-1;0); IF(ROWS($E$3:E3)=1; -OFFSET($E$2;$H$2;0);D3/SQRT($H$5))))))

Número de Amostras - n | Célula H2

=CONT.NÚM(B:B)

ou em inglês

=COUNT(B:B)

u | Célula H3

=(1/RAIZ($H$2))

ou em inglês

=(1/SQRT($H$2))

m | Célula H4

=SOMAQUAD(D:D)

ou em inglês

=SUMSQ(D:D)

e | Célula H5

=(H4-2*DESLOC($D$2;$H$2;0)^2 -2*DESLOC($D$2;$H$2-1;0)^2)/ (1-2*DESLOC($E$2;$H$2;0)^2 -2*DESLOC($E$2;$H$2-1;0)^2)

ou em inglês

=(H4-2*OFFSET($D$2;$H$2;0)^2 -2*OFFSET($D$2;$H$2-1;0)^2)/ (1-2*OFFSET($E$2;$H$2;0)^2 -2*OFFSET($E$2;$H$2-1;0)^2)

W | Célula H7

=CORREL(MENOR(DESLOC($B$2;1;0;H2;1);LIN(INDIRETO("1:"&$H$2)));DESLOC($E$2;1;0;$H$2;1))^2

ou em inglês

=CORREL(SMALL(OFFSET($B$2;1;0;H2;1);ROW(INDIRECT("1:"&$H$2)));OFFSET($E$2;1;0;$H$2;1))^2

mean | Célula H8

=0,0038915*LN($H$2)^3 -0,083751*LN($H$2)^2 -0,31082*LN($H$2)-1,5861

stdev | Célula H9

=EXP(0,0030301*LN($H$2)^2 -0,082676*LN($H$2) -0,4803)

Z | Célula H10

=PADRONIZAR(LN(1-H7);H8;H9)

ou em inglês

=STANDARDIZE(LN(1-H7);H8;H9)

p-value | Célula H11

=1-DIST.NORMP(H10)

ou em inglês

=1-NORMSDIST(H10)

Rejeita | Célula H13

=SE(H11<=H12;"Sim";"Não")

ou em inglês

=IF(H11<=H12;"Sim";"Não")

Média | Célula H15

=MÉDIA(B:B)

ou em inglês

=AVERAGE(B:B)

Variância | Célula H16

=VAR(B:B)

Skewness | Célula H18

=DISTORÇÃO(B:B)

ou em inglês

=SKEW(B:B)

Excess kurtosis | Célula H19

=CURT(B:B)

ou em inglês

=KURT(B:B)

Espero que tenha gostado desse artigo!

Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.

Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.

E ja conhece o meu novo curso online de Excel?

Abraços a todos e até o próximo artigo!

Fabio BALDINI

Frase do Dia: "Estudar e não pensar é desperdício. Pensar e não estudar é perigoso" Autor: Confusio