▷ Métricas de Erros Estatísticos no Excel

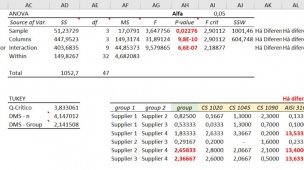
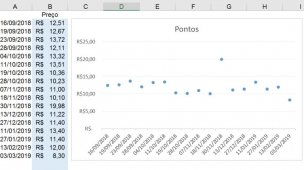
Olá seja bem vindo ao meu artigo

Medir a precisão da previsão (ou erro) não é tarefa fácil, pois não há somente um indicador.

Mas antes temos que fazer uma distinção entre a precisão e seu viés

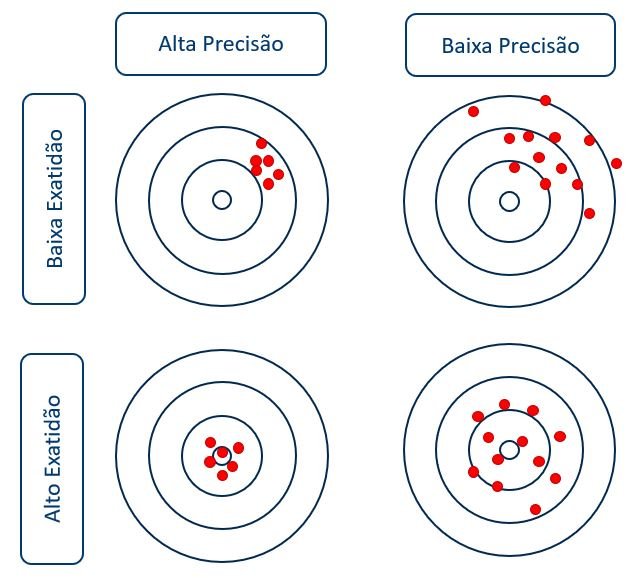
Precisão: É o grau de variação dos resultados. Não é o mesmo que exatidão. A precisão fornece uma ideia da magnitude do erro, mas não da direção.

Viés (exatidão): É o grau da direção do erro, representa o erro médio histórico.

Como pode ver na figura abaixo, o que se deseja é uma previsão precisa e direcionada.

Neste post vou descrever as principais métricas de erros utilizada em análises estatísticas existentes na literatura.

As mensurações dos erros são importantes para verificar se a assertividade do modelo está convergindo ou não, em nossas previsões ou na comparação entre informações.

Vamos aos cálculos

n-Real (Quantidade de Amostras) | Célula F3

=CONT.NÚM(B:B)

ou em inglês

=COUNT(B:B)

n-Previsão(Quantidade de Amostras) | Célula F4

=CONT.NÚM(C:C)

ou em inglês

=COUNT(C:C)

Com os as quantidades corretas de amostras, vamos aos cálculos dos erros

ME/Bias | Célula F6

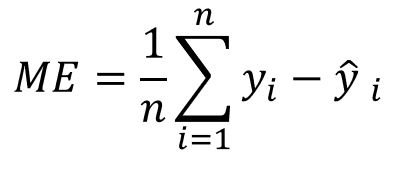
ME = Mean Error/Bias | Erro Médio / Viés

A utilização deste erro, está sujeito a valores positivos e negativos que podem se anular.

=MÉDIA(ÍNDICE(DESLOC($C$5;0;0;F4;1)-DESLOC($B$5;0;0;F4;1);0))

ou em inglês

=AVERAGE(INDEX(OFFSET($C$5;0;0;F4;1)-OFFSET($B$5;0;0;F4;1);0))

SE | Célula F7

SE = Standard Forecast Error | Erro Padrão da Previsão

=MÉDIA(ÍNDICE((DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))^2;0))-(MÉDIA(ÍNDICE(DESLOC($C$5;0;0;F4;1)-DESLOC($B$5;0;0;F4;1);0)))^2

ou em inglês

=AVERAGE(INDEX((OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))^2;0))-(AVERAGE(INDEX(OFFSET($C$5;0;0;F4;1)-OFFSET($B$5;0;0;F4;1);0)))^2

MAE/MAD | Célula F8

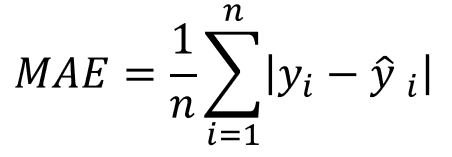
MAE/MAD = Mean Absolute Error/Mean Absolute Deviation | Erro Médio Absoluto

Este erro é dependente de escala, resultando na diferença absoluta, não possui o efeito da anulação dos valores dos positivos e negativos.

=MÉDIA(ÍNDICE(ABS(DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1));0))

ou em inglês

=AVERAGE(INDEX(ABS(OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1));0))

MSE | Célula F9

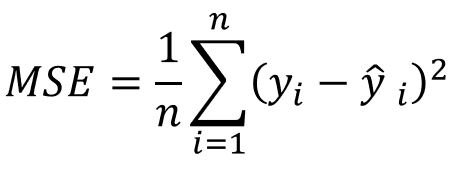
MSE = Mean Square Error | Erro Médio Quadrático

=MÉDIA(ÍNDICE((DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))^2;0))

ou em inglês

=AVERAGE(INDEX((OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))^2;0))

RMSE | Célula F10

RMSE = Root Mean Square Error | Raiz do Quadrado Médio do Erro

Este erro é independente de escala, quanto menor o valor, melhor.

=RAIZ(MÉDIA(ÍNDICE((DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))^2;0)))

ou em inglês

=SQRT(AVERAGE(INDEX((OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))^2;0)))

MPE | Célula F11

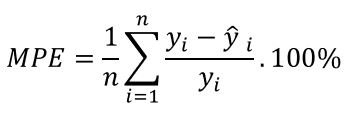
MPE = Mean Percentage Error | Erro Médio Percentual

Independente de escala, este erro resulta a taxa de erro em percentual

=MÉDIA(ÍNDICE((DESLOC($C$5;0;0;F4;1)-DESLOC($B$5;0;0;F4;1))/DESLOC($B$5;0;0;F4;1);0))*100

ou em inglês

=AVERAGE(INDEX((OFFSET($C$5;0;0;F4;1)-OFFSET($B$5;0;0;F4;1))/OFFSET($B$5;0;0;F4;1);0))*100

MAPE | Célula F12

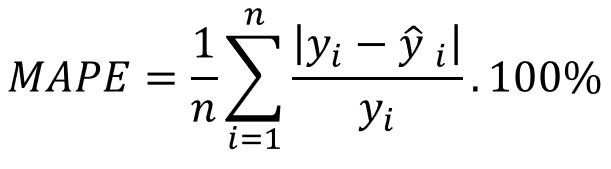
MAPE = Mean Absolute Percentage Error | Erro Médio Percentual Absoluto

Independente de escala, este erro resulta a taxa de erro em percentual absoluto, sendo a média dos erros percentuais.

=MÉDIA(ÍNDICE(ABS(DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))/DESLOC($B$5;0;0;F4;1);0))*100

ou em inglês

=AVERAGE(INDEX(ABS(OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))/OFFSET($B$5;0;0;F4;1);0))*100

SMAPE | Célula F13

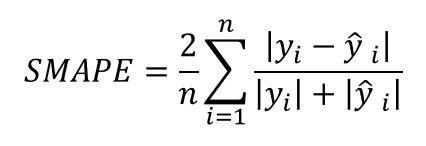
SMAPE = Symmetric Mean Absolute Percentage Error | Erro Percentual Absoluto Médio Simétrico

Chen e Yang (2004) definiram este tipo de erro, sendo que outros autores propuseram outro cálculo para esta definição.

=MÉDIA(ÍNDICE(2*ABS(DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))/(ABS(DESLOC($B$5;0;0;F4;1))+ABS(DESLOC($C$5;0;0;F4;1)));0))

ou em inglês

=AVERAGE(INDEX(2*ABS(OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))/(ABS(OFFSET($B$5;0;0;F4;1))+ABS(OFFSET($C$5;0;0;F4;1)));0))

MASE | Célula F14

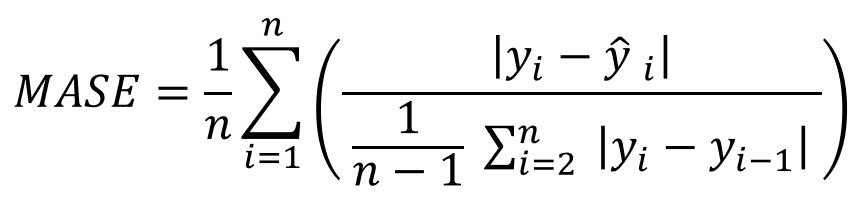
MASE = Mean Absolute Scaled Error | Erro Médio Absoluto em Escala

Quanto menor o valor do MASE, menor o erro relativo absoluto da previsão.

=MÉDIA(ÍNDICE(ABS(DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))/(SOMA(ÍNDICE(ABS(DESLOC($B$5;1;0;F4-1;1)-DESLOC($B$5;0;0;F4-1;1));0))/(F4-1));0))

ou em inglês

=AVERAGE(INDEX(ABS(OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))/(SUM(INDEX(ABS(OFFSET($B$5;1;0;F4-1;1)-OFFSET($B$5;0;0;F4-1;1));0))/(F4-1));0))

GRMSE | Célula F15

GRMSE = Geometric Root Mean Square Error | Erro Geométrico da Raiz Quadrada Média

Este erro é mais robusto que o RMSE e menos afetado por valores discrepantes.

=PRODUTO(ÍNDICE((DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))^2;0))^(1/(2*F4))

ou em inglês

=PRODUCT(INDEX((OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))^2;0))^(1/(2*F4))

MAAPE | Célula F16

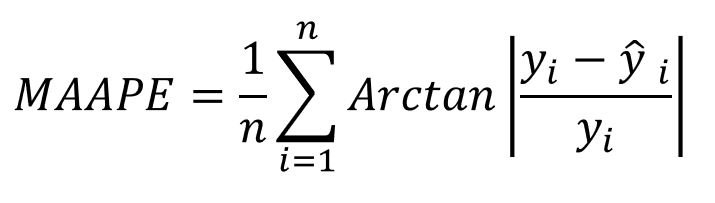
MAAPE = Mean Arctangent Absolute Percentage Error | Erro Percentual Absoluto Médio Arco-Tangente

Este erro não possui uma versão simétrica e não contém escala, pois seus valores são expressos em radianos.

=MÉDIA(ÍNDICE(ATAN(ABS((DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))/(DESLOC($B$5;0;0;F4;1))));0))

ou em inglês

=AVERAGE(INDEX(ATAN(ABS((OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))/(OFFSET($B$5;0;0;F4;1))));0))

Theil's U | Célula F17

O "U" de Theil é uma estatística usada para avaliar se um modelo de previsão é ou não superior à previsão ingênua. Valores menores que 1 indicam que o modelo é superior, enquanto valores maiores que 1 indicam que o modelo é pior que a previsão ingênua. A estatística é calculada como a raiz quadrada da proporção da soma dos erros quadráticos, modelo de previsão para previsão ingênua.

Verificando que este erro é necessário utilizar um período antes da série avaliada, devido a isso do deslocamento da previsão em comparação ao real.

=RAIZ(ÍNDICE(SOMA(((DESLOC($C$5;0;0;F4;1)-DESLOC($B$5;0;0;F4;1))/(DESLOC($B$5;-1;0;F4;1)))^2)/SOMA(((DESLOC($B$5;0;0;F4;1)-DESLOC($B$5;-1;0;F4;1))/(DESLOC($B$5;-1;0;F4;1)))^2);0))

ou em inglês

=SQRT(INDEX(SUM(((OFFSET($C$5;0;0;F4;1)-OFFSET($B$5;0;0;F4;1))/(OFFSET($B$5;-1;0;F4;1)))^2)/SUM(((OFFSET($B$5;0;0;F4;1)-OFFSET($B$5;-1;0;F4;1))/(OFFSET($B$5;-1;0;F4;1)))^2);0))

Theil's U' 2 | Célula F18

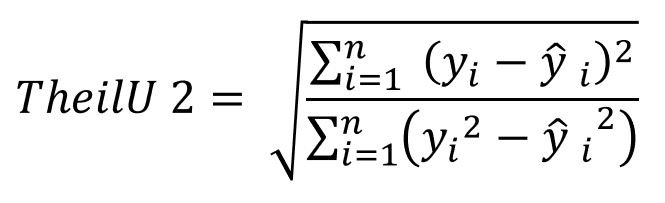
=RAIZ(ÍNDICE(SOMA((DESLOC($B$5;0;0;F4;1)-DESLOC($C$5;0;0;F4;1))^2)/SOMA(((DESLOC($B$5;0;0;F4;1))^2)+((DESLOC($C$5;0;0;F4;1))^2));0))

ou em inglês

=SQRT(INDEX(SUM((OFFSET($B$5;0;0;F4;1)-OFFSET($C$5;0;0;F4;1))^2)/SUM(((OFFSET($B$5;0;0;F4;1))^2)+((OFFSET($C$5;0;0;F4;1))^2));0))

R² | Célula F19

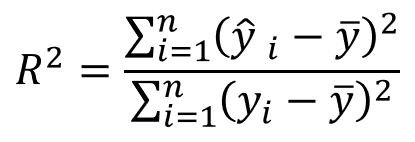
R² = Square R | R Quadrado

Utilizado na estatística inferencial, este erro mede o quanto que uma variável explica sobre a variação da outra.

=SOMA(ÍNDICE((DESLOC($B$5;0;0;F4;1)-MÉDIA(DESLOC($B$5;0;0;F4;1)))^2;0))/SOMA(ÍNDICE((DESLOC($C$5;0;0;F4;1)-MÉDIA(DESLOC($B$5;0;0;F4;1)))^2;0))

ou em inglês

=SUM(INDEX((OFFSET($B$5;0;0;F4;1)-AVERAGE(OFFSET($B$5;0;0;F4;1)))^2;0))/SUM(INDEX((OFFSET($C$5;0;0;F4;1)-AVERAGE(OFFSET($B$5;0;0;F4;1)))^2;0))

Espero que tenha gostado desse artigo!

Caso queria saber mais sobre as Métricas de Erros segue o link abaixo, um artigo muito bom!

https://medium.com/analytics-vidhya/forecast-kpi-rmse-mae-mape-bias-cdc5703d242d

Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.

Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.

E ja conhece o meu novo curso online de Excel?

Abraços a todos e até o próximo artigo!

Fabio BALDINI

Frase do Dia: "Aquele que pensa positivo vê o invisível, sente o intangível e alcança o impossível" Autor: Winston Churchill