Olá seja bem vindo ao meu mais novo artigo
O método MAUT - Multi-Attribute Utility Theory (Teoria da Utilidade Multi-Atributo) foi introduzido por Keeney e Raiffa em 1976. A simplicidade na resolução de múltiplos atributos problemas de tomada de decisão é uma das vantagens desta técnica, e dá
abundante liberdade de ação para os tomadores de decisão para tornar o resultado mais preciso e realista. O método MAUT tem o seguinte recursos:
• Este método pertence aos métodos compensatórios;
• Os atributos são independentes uns dos outros;
• Os atributos qualitativos são convertidos em atributos quantitativos;
• Simples a sua aplicação.
No exemplo abaixo será demonstrado uma aplicação com 4 critérios e 4 alternativas;
Vamos ao método MAUT passo a passo;
1° Etapa
Definição dos critérios de Maximização ou Minimização e seus pesos;
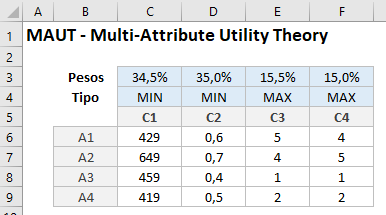
2° Etapa
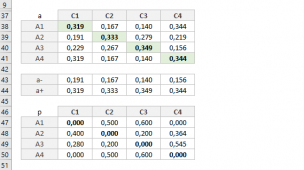
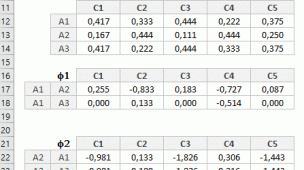
Criar a Matriz de Pontuação de Vantagem Marginal normalizada para o método MAUT

segue a fórmula iniciando na Célula C13
=(EXP(SE(C$4="MIN";1+(MÍNIMO(C$6:C$9)-C6)/(MÁXIMO(C$6:C$9)-MÍNIMO(C$6:C$9));(C6-MÍNIMO(C$6:C$9))/(MÁXIMO(C$6:C$9)-MÍNIMO(C$6:C$9)))^2)-1)/1,71ou em inglês
=(EXP(SE(C$4="MIN";1+(MÍNIMO(C$6:C$9)-C6)/(MÁXIMO(C$6:C$9)-MÍNIMO(C$6:C$9));(C6-MÍNIMO(C$6:C$9))/(MÁXIMO(C$6:C$9)-MÍNIMO(C$6:C$9)))^2)-1)/1,713° Etapa
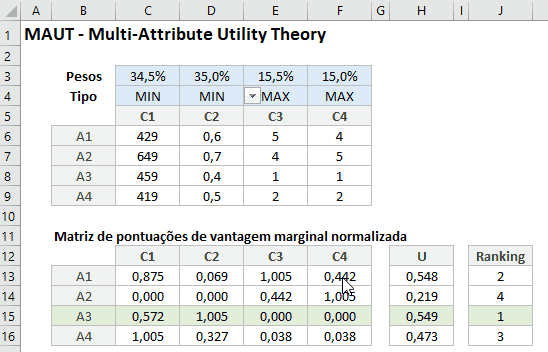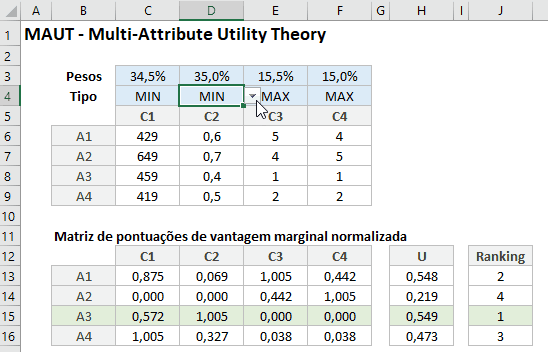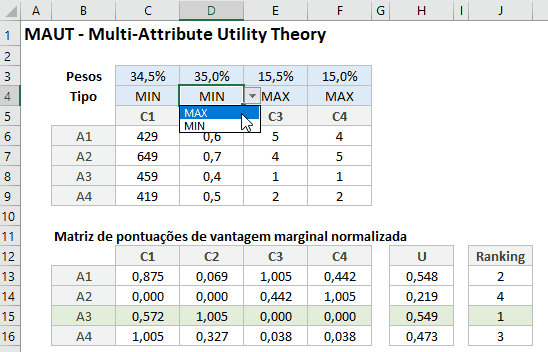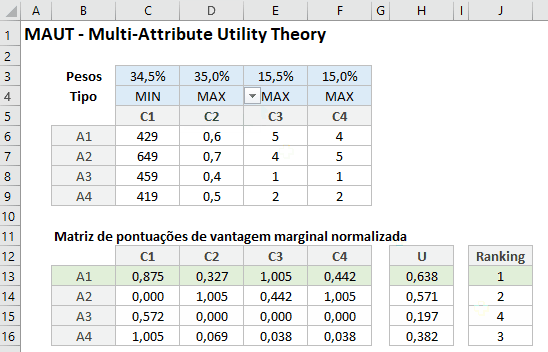
Após a criação da Matriz, é necessário calcular a pontuação de vantagem final e o ranking

Segue a fórmula na célula H13 da pontuação de vantagem final U
=SOMARPRODUTO(C13:F13;$C$3:$F$3)ou em inglês
=SUMPRODUCT(C13:F13;$C$3:$F$3)O Ranking final do Método MAUT, segue a fórmula na célula J13
=ORDEM(H13;$H$13:$H$16)ou em inglês
=RANK(H13;$H$13:$H$16)Segue o método MAUT Dinâmico!
Espero que tenha gostado desse artigo!
Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.
Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.
Venha fazer o melhor curso EAD de Excel comigo! Clique e compare!

Abraços a todos e até o próximo artigo!
Fabio BALDINI
Frase do Dia: "Tudo seria muito fácil, se não fossem as dificuldades!" Autor: Barão de Itararé