▷ WINGS no Excel – Weighted Influence Non-linear Gauge System

Olá seja bem vindo ao meu novo artigo

Será demonstrado uma técnica de auxílio a decisão multicritério chamada WINGS (Weighted Influence Non-linear Gauge System) criado por Jerzy Michnik (2013) em seu artigo abaixo

https://www.researchgate.net/publication/235780422_Weighted_Influence_Non-linear_Gauge_System_WINGS_-_An_analysis_method_for_the_systems_of_interrelated_components

Este método foi criado a partir da necessidade de considerar não somente a influência entre os critérios, demonstrada no método DEMATEL, mas a força relativa (importância) dentro do sistema analisado.

"Weighted" significa que a importância (força interna) dos critérios modificam a influência, que possuem peso;

"Influence" atribui o papel das relações entre os critérios.

"Gauge System" indica que o método é um sistema de medição.

Algumas considerações, as fórmulas estão fixadas com até 50 critérios e 5 escalas de influência, sendo possível aumentar para o limite do Excel. Foi utilizado a função UNIDM / MUNIT esta função retorna a matriz identidade e ela só está disponível no Office 365.

Este método foi apresentado pelo Prof. Dr. Marcos Santos e pelo seu aluno Mestrando Igor Pinheiro de Araújo Costa.

Vamos aos passos

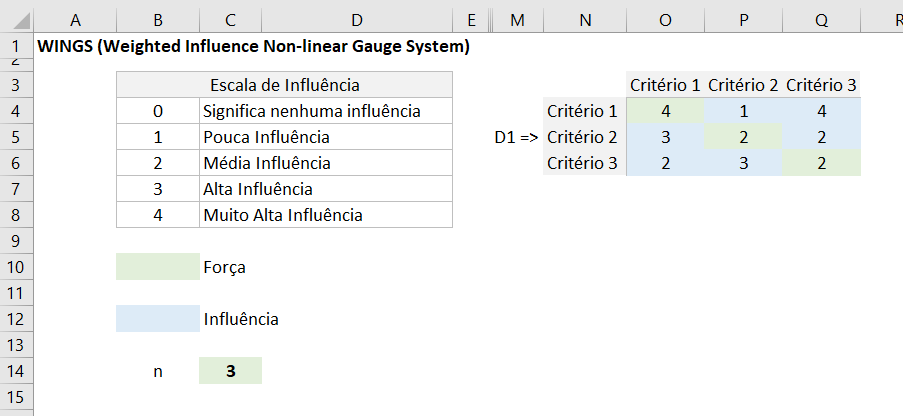
1° Passo - Definir a Escala de Influência

2° Passo - Criação da Matriz D

Nesta etapa para a criação da Matriz D será necessário atribuir as forças e influências entre os critérios, somente na diagonal principal (cor verde) deverá preencher o valor da Força entre os critérios e nas células restantes o valor da influência (cor azul), o quanto um critério tem influência sobre o outro.

3° Passo - Calcular a Matriz T

Para a criação da Matriz de relacionamento total T = D*(I-D)^-1, sendo que I é a Matriz Identidade.

Segue as fórmulas de todos os elementos da Matriz T iniciando na célula BP4

=SE(E(LINS(O$4:O4)<=$C$14;COLS($O4:O4)<=$C$14);ÍNDICE(MATRIZ.MULT(
DESLOC($N$3;1;1;$C$14;$C$14)/SOMA(DESLOC($N$3;1;1;$C$14;$C$14));
MATRIZ.INVERSO(MUNIT($C$14)-(DESLOC($N$3;1;1;$C$14;$C$14)/
SOMA(DESLOC($N$3;1;1;$C$14;$C$14)))));LINS($O$4:O4);COLS($O$4:O4));"")

ou em inglês

=IF(AND(ROWS(O$4:O4)<=$C$14;COLUMNS($O4:O4)<=$C$14);INDEX(MMULT(
OFFSET($N$3;1;1;$C$14;$C$14)/SUM(OFFSET($N$3;1;1;$C$14;$C$14));
MINVERSE(MUNIT($C$14)-(OFFSET($N$3;1;1;$C$14;$C$14)/
SUM(OFFSET($N$3;1;1;$C$14;$C$14)))));ROWS($O$4:O4);COLUMNS($O$4:O4));"")

4° Passo - Calcular os índices finais

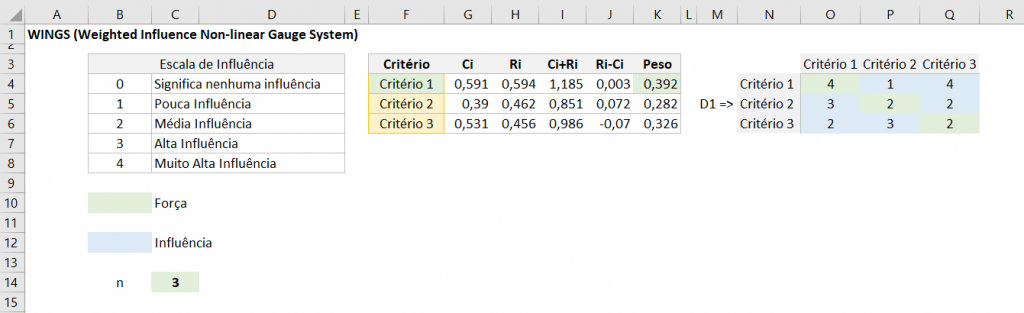
Com a matriz criada T podemos obter os coeficientes Ci e Ri

Ci - Soma dos índices por coluna para os critérios - Coluna G

=SE($C$14<LINS($G$4:G4);"";SOMA(DESLOC($BO$3;1;LINS($G$4:G4);$C$14;1)))

ou em inglês

=IF($C$14<ROWS($G$4:G4);"";SUM(OFFSET($BO$3;1;ROWS($G$4:G4);$C$14;1)))

Ri - Soma dos índices por linha para os critérios - Coluna H

=SE($C$14<LINS($H$4:H4);"";SOMA(DESLOC($BO$3;LINS($H$4:H4);1;1;$C$14)))

ou em inglês

=IF($C$14<ROWS($H$4:H4);"";SUM(OFFSET($BO$3;ROWS($H$4:H4);1;1;$C$14)))

Ci+Ri - Coluna I

=SE($C$12<LINS($I$4:I4);"";G4+H4)

ou em inglês

=IF($C$14<ROWS($I$4:I4);"";G4+H4)

Ri-Ci - Coluna J

=SE($C$14<LINS($J$4:J4);"";H4-G4)

ou em inglês

=IF($C$14<ROWS($J$4:J4);"";H4-G4)

Peso - Coluna K

=SE($C$14<LINS($K$4:K4);"";I4/SOMA($I$4:$I$53))

ou em inglês

=IF($C$14<ROWS($K$4:K4);"";I4/SUM($I$4:$I$53))

Agora a técnica WINGS que auxilia a tomada de decisão com multicritérios de maneira dinâmica

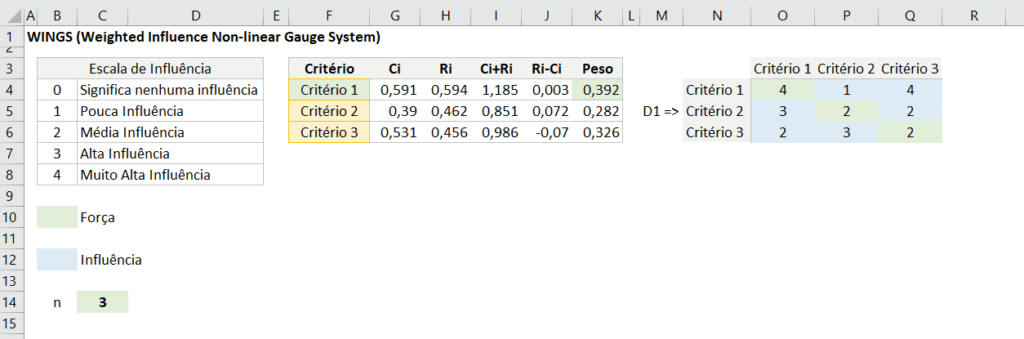
Segue o link abaixo para você poder baixar o arquivo

O mesmo foi patenteado sob o Processo de Número BR5120200001828-9, apenas para uso acadêmico e 100% gratuito e uso não comercial

Gostaria de fazer um agradecimento em especial ao Prof. Dr. Marcos Santos e ao Mestrando Igor Pinheiro de Araújo Costa, pela apresentação da técnica.

Espero que tenha gostado desse artigo!

Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.

Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.

E você já conhece o meu novo Curso de Excel EAD?

Abraços a todos e até o próximo artigo!

Fabio BALDINI

Frase do Dia: "Sempre tenha em mente que sua própria determinação para com o sucesso é mais importante do que qualquer outra coisa" Autor: Abraham Lincoln