Olá seja bem vindo ao meu mais novo artigo
Neste artigo irei descrever o cálculo dos três métodos ordinais multicritérios de Borda, Condorcet e Copeland.
Antes quero agradecer imensamente ao Prof. Dr. Marcos Santos por disponibilizar o método passo a passo na nossa live pelo Instituto X
uma breve descrição sobre os três métodos, vamos a eles:
Método Borda
O método foi proposto por Jean Charles de Borda (1733-1799), sendo que este método utiliza a escala ordinal.
As alternativas ganham uma ordenação por meio de pontuação, sendo que a alternativa que obtiver a menor pontuação é a que será escolhida
Este método é compensatório, pois ele pode ter uma nota ruim em um critério mas pode haver uma nota boa em outro critério e por isso que este método compensa a nota final atribuída.
1° Passo - Definir a escala de avaliação

2° Passo - Definir os dados de entrada e a Opção de Maximização ou Minimização por critério
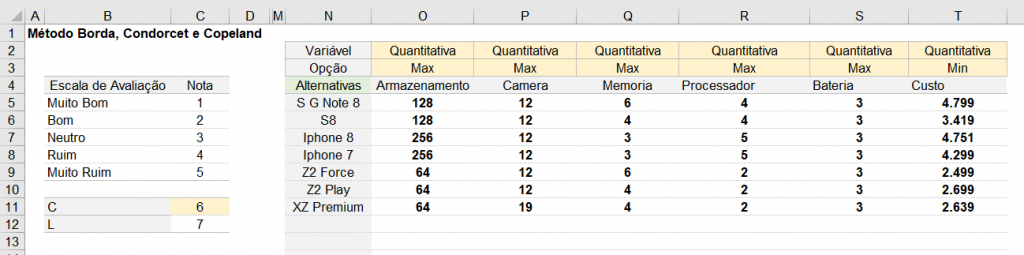
3° Passo - Criação da Matriz para o Método de Borda

Segue a fórmula que inicia na célula O28
=SE(O5="";"";SE(OU(O$3="Max";O$3="");SOMA(ÍNDICE((O5<=DESLOC(
O$4;1;0;$C$12;1))/CONT.SE(DESLOC(O$4;1;0;$C$12;1);DESLOC(
O$4;1;0;$C$12;1));0));SOMA(ÍNDICE((O5>=DESLOC(O$4;1;0;$C$12;1)
)/CONT.SE(DESLOC(O$4;1;0;$C$12;1);DESLOC(O$4;1;0;$C$12;1));0))))ou em inglês
=IF(O5="";"";IF(OR(O$3="Max";O$3="");SUM(INDEX((O5<=OFFSET(
O$4;1;0;$C$12;1))/COUNTIF(OFFSET(O$4;1;0;$C$12;1);OFFSET(
O$4;1;0;$C$12;1));0));SUM(INDEX((O5>=OFFSET(O$4;1;0;$C$12;1)
)/COUNTIF(OFFSET(O$4;1;0;$C$12;1);OFFSET(O$4;1;0;$C$12;1));0))))4° Passo - Somar e Ranquear as alternativas
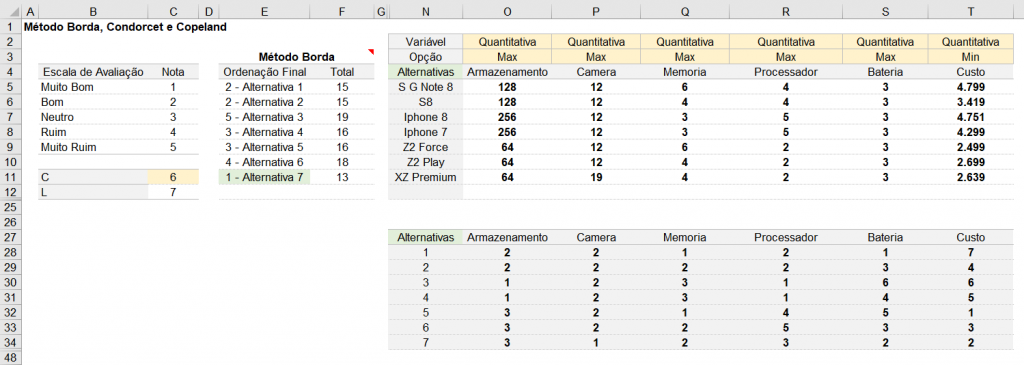
Para realizar a soma das alternativas segue a fórmula na coluna F
=SE(N28="";"";SOMA(O28:AH28))ou em inglês
=IF(N28="";"";SUM(O28:AH28))Para o ranqueamento de qual critério é o melhor, segue a fórmula na coluna E
=SE(N28="";"";SEERRO(SOMA(ÍNDICE((F5>=DESLOC(F$4;1;0;$C$12;1))
/CONT.SE(DESLOC(F$4;1;0;$C$12;1);DESLOC(F$4;1;0;$C$12;1));0))
&" - Alternativa "&N28;""))ou em inglês
=IF(N28="";"";IFERROR(SUM(INDEX((F5>=OFFSET(F$4;1;0;$C$12;1))
/COUNTIF(OFFSET(F$4;1;0;$C$12;1);OFFSET(F$4;1;0;$C$12;1));0))
&" - Alternativa "&N28;""))Como demonstrado, a melhor alternativa é a que terá a menor pontuação entre os critérios.
Método Condorcet e Copeland
O método de Condorcet foi idealizado por Jean-Marie Antoine Nicolas de Caritat, Marquês de Condorcet (1743-1794), este método trabalha com relações de superação/sobreclassificação. Sendo que este método pode conduzir ao ciclo de Intransitividade ou "paradoxo de Condorcet".
O método de Copeland é uma evolução do método de Condorcet, onde o procedimento é igual ao Condorcet até a matriz de decisão, somente o último cálculo será modificado.
Vamos aos passos destes métodos
1° Passo - Definir a escala de avaliação

2° Passo - Definir os dados de entrada e a Opção de Maximização ou Minimização por alternativa
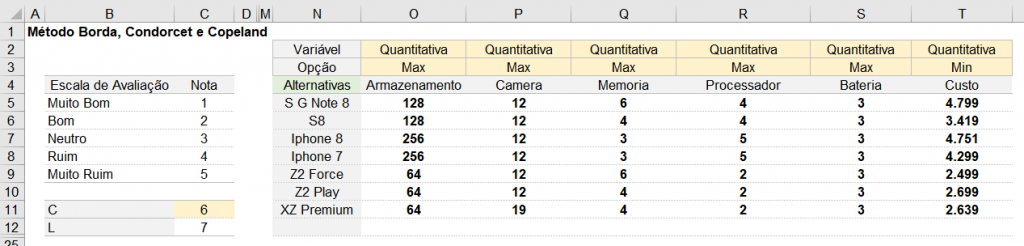
3° Passo - Criar a matriz para cada critério
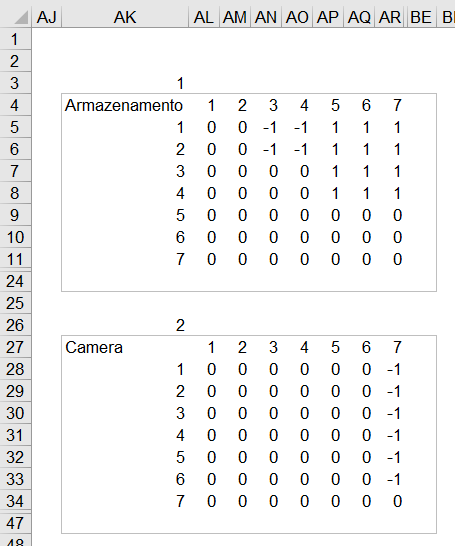
Nesta etapa foram criadas 20 matrizes para cada critério de entrada, sendo utilizado somente 6 que foi o exercício proposto.
Segue a fórmula na célula AL5
=SE(OU(AL$4="";$AK5="");"";SE(OU($AK5=AL$4;$AK5>AL$4);0;SE(
DESLOC($N$27;$AK5;$AK$3)>DESLOC($N$27;AL$4;$AK$3);-1;SE(
DESLOC($N$27;$AK5;$AK$3)=DESLOC($N$27;AL$4;$AK$3);0;1))))ou em inglês
=IF(OR(AL$4="";$AK5="");"";IF(OR($AK5=AL$4;$AK5>AL$4);0;IF(
OFFSET($N$27;$AK5;$AK$3)>OFFSET($N$27;AL$4;$AK$3);-1;IF(
OFFSET($N$27;$AK5;$AK$3)=OFFSET($N$27;AL$4;$AK$3);0;1))))Criada todas as matrizes dos critérios é necessário criar a ultima matriz.
4° Passo - Criar a Matriz de Decisão
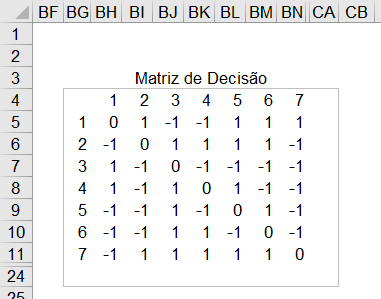
Segue as fórmulas para a criação da matriz de decisão iniciando na célula BH5
=SE(OU(BH$4="";$BG5="");"";SE($BG5=BH$4;0;SE($BG5>BH$4;
-DESLOC($BG$4;BH$4;$BG5);SE(SOMASE($AK$5:$AK$461;$BG5;
AL$5:AL$461)>1;1;SE(SOMASE($AK$5:$AK$461;$BG5;AL$5:AL$461)
<-1;-1;SOMASE($AK$5:$AK$461;$BG5;AL$5:AL$461))))))ou em inglês
=IF(OR(BH$4="";$BG5="");"";IF($BG5=BH$4;0;IF($BG5>BH$4;
-OFFSET($BG$4;BH$4;$BG5);IF(SUMIF($AK$5:$AK$461;$BG5;
AL$5:AL$461)>1;1;IF(SUMIF($AK$5:$AK$461;$BG5;AL$5:AL$461)
<-1;-1;SUMIF($AK$5:$AK$461;$BG5;AL$5:AL$461))))))5° Passo - Ranquear os Métodos Condorcet e Copeland
Para cada método haverá um cálculo, vamos a eles

Método de Condorcet - Coluna I
=SE(N28="";"";CONT.SE(BH5:CA5;">0"))ou em inglês
=IF(N28="";"";COUNTIF(BH5:CA5;">0"))Ordenação das alternativas - Coluna H
=SE(N28="";"";SEERRO(SOMA(ÍNDICE((I5<=DESLOC(I$4;1;0;$C$12;1)
)/CONT.SE(DESLOC(I$4;1;0;$C$12;1);DESLOC(I$4;1;0;$C$12;1));0)
)&" - Alternativa "&N28;""))ou em inglês
=IF(N28="";"";IFERROR(SUM(INDEX((I5<=OFFSET(I$4;1;0;$C$12;1)
)/COUNTIF(OFFSET(I$4;1;0;$C$12;1);OFFSET(I$4;1;0;$C$12;1));0)
)&" - Alternativa "&N28;""))Método de Copeland - Coluna L
=SE(N28="";"";SOMA(BH5:CA5))ou em inglês
=IF(N28="";"";SUM(BH5:CA5))Ordenação das Alternativas - Coluna K
=SE(N28="";"";SEERRO(SOMA(ÍNDICE((L5<=DESLOC(L$4;1;0;$C$12;1)
)/CONT.SE(DESLOC(L$4;1;0;$C$12;1);DESLOC(L$4;1;0;$C$12;1));0)
)&" - Alternativa "&N28;""))ou em inglês
=IF(N28="";"";IFERROR(SUM(INDEX((L5<=OFFSET(L$4;1;0;$C$12;1)
)/COUNTIF(OFFSET(L$4;1;0;$C$12;1);OFFSET(L$4;1;0;$C$12;1));0)
)&" - Alternativa "&N28;""))Segue os três métodos de Borda, Condorcet e Copeland que irá de auxiliar na tomada de decisão multicritério.

Segue o link abaixo para realizar o download do arquivo
O mesmo foi realizado o Registro de Software sob o Processo de Número BR5120200002442-4, apenas para uso acadêmico e 100% gratuito e uso não comercial
Espero que tenha gostado desse artigo!
Gostaria de fazer um agradecimento novamente em especial ao Prof. Dr. Marcos Santos pela apresentação da técnica.
Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.
Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.
E você já conhece o meu novo Curso de Excel EAD?

Abraços a todos e até o próximo artigo!
Fabio BALDINI
Frase do Dia: "A questão não é quem vai deixar eu fazer, e sim quem vai me tentar me parar" Autor: Ayn Rand




Link permanente