Olá seja bem vindo ao meu mais novo artigo
O método proposto é denominado CODAS, que significa COmbinative Distance-based ASsessment (Avaliação Combinativa à Distância). Neste método, a conveniência de alternativas é determinada usando duas medidas. A medida principal e primária está relacionada à distância euclidiana das alternativas do ideal-negativo. Usar esse tipo de distância requer um espaço de indiferença para os critérios. A medida secundária é a distância do Taxicab (Manhattan), que está relacionada ao espaço de indiferença. É claro que a alternativa que tem maiores distâncias da solução do ideal negativo é mais desejável. Neste método, se tivermos duas alternativas incomparáveis de acordo com a distância euclidiana, a distância do táxi é usada como medida secundária. Embora o espaço de indiferença seja preferido no CODAS, dois tipos de espaço de indiferença podem ser considerados em seu processo.
No exemplo abaixo será demonstrado uma aplicação com 7 critérios e 7 alternativas. As etapas do método proposto são apresentadas a seguir:
Vamos ao método CODAS passo a passo
1° Etapa
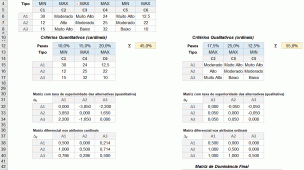
Definir os Pesos de cada critério e se o critério é de Maximização ou Minimização,

2° Etapa
Criar a Matriz Normalizada e Ponderada

Segue a fórmula iniciando na célula C16
=SE(C$4="MAX";C6/MÁXIMO(C$6:C$12);MÍNIMO(C$6:C$12)/C6)*C$3ou em inglês
=IF(C$4="MAX";C6/MAX(C$6:C$12);MIN(C$6:C$12)/C6)*C$33° Etapa
Calcular os índices Minimos, Ei, Ti, e Phi

Segue a fórmula do Mínimo iniciando na célula C24
=MÍNIMO(C16:C22)ou em inglês
=MIN(C16:C22)Segue o cálculo do Índice Ei (Distância Euclidiana) iniciando na célula K16
=RAIZ(SOMAXMY2(C16:I16;$C$24:$I$24))ou em inglês
=SQRT(SUMXMY2(C16:I16;$C$24:$I$24))Segue o cálculo do Índice Ti (Distância Taxicab/Manhattan) iniciando na célula M16
=(SOMA(ABS(C16:I16-$C$24:$I$24)))ou em inglês
=(SUM(ABS(C16:I16-$C$24:$I$24)))o Phi será utilizado na construção da Matriz de Avaliação Relativa que iremos fixar em 0,02 (célula O16)
4° Etapa
Construir a matriz de Avaliação Relativa

Segue a fórmula iniciando na célula C29
=(ÍNDICE($K$16:$K$22;CORRESP($B29;$B$16:$B$22;0))-ÍNDICE($K$16:$K$22;CORRESP(C$27;$B$16:$B$22;0)))+($O$16*(ÍNDICE($K$16:$K$22;CORRESP($B29;$B$16:$B$22;0))-ÍNDICE($K$16:$K$22;CORRESP(C$27;$B$16:$B$22;0)))*(ÍNDICE($M$16:$M$22;CORRESP($B29;$B$16:$B$22;0))-ÍNDICE($M$16:$M$22;CORRESP(C$27;$B$16:$B$22;0))))ou em inglês
=(INDEX($K$16:$K$22;MATCH($B29;$B$16:$B$22;0))-INDEX($K$16:$K$22;MATCH(C$27;$B$16:$B$22;0)))+($O$16*(INDEX($K$16:$K$22;MATCH($B29;$B$16:$B$22;0))-INDEX($K$16:$K$22;MATCH(C$27;$B$16:$B$22;0)))*(INDEX($M$16:$M$22;MATCH($B29;$B$16:$B$22;0))-INDEX($M$16:$M$22;MATCH(C$27;$B$16:$B$22;0))))Utilizei a linha 27 para acelerar os cálculos
E somente falta realizar a soma na iniciando na célula K29
=SOMA(C29:I29)ou em inglês
=SUM(C29:I29)5° Etapa
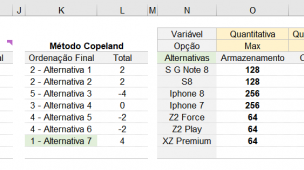
Realizar o Ranking das alternativas

Que segue iniciando na célula M29
=ORDEM(K29;$K$29:$K$35)ou em inglês
=RANK(K29;$K$29:$K$35)
Espero que tenha gostado desse artigo!
Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.
Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.
Venha fazer o melhor curso EAD de Excel comigo! Clique e compare!

Abraços a todos e até o próximo artigo!
Fabio BALDINI
Frase do Dia: " Eu não sonhei com o sucesso. Eu trabalhei para ele. " Autor: Estée Lauder