Olá pessoal, bem vindo ao meu novo artigo! Fazendo um curso sobre bolsa de valores me apresentaram a técnica de precificação de opções chamada Black & Scholes e suas "gregas"
Segue o link abaixo com a definição e os conceitos utilizado nesta técnica no artigo abaixo
Em resumo, este modelo serve para precificar as nossas "opções" e verificar os parâmetros de Delta, Gamma, Theta, Vega e Rho, que são chamadas de "gregas". Mas antes, precisamos da definição do conceito de "Call" e "Put",
CALL - É o direito de compra de um ativo em uma data futura, chamado opção de compra.
PUT - É o direito de venda de um ativo em uma data futura, chamado opção de venda.
Para a realização do cálculo serão necessários alguns valores, que são eles
S - Valor da ação na presente data
K ou X - Valor do preço de exercício da opção
r - Taxa de Juros de Risco (neste caso será a SELIC)
T - Intervalo de tempo até a expiração, em fração de ano 365 dias ou 252 dias úteis
V - Volatilidade da ação (quanto que ela varia ao longo de um período)

Com esses dados, teremos que calcular todas as "Gregas" (Delta, Gamma, Theta, Vega e Rho) para as opções "Call" e "Put".
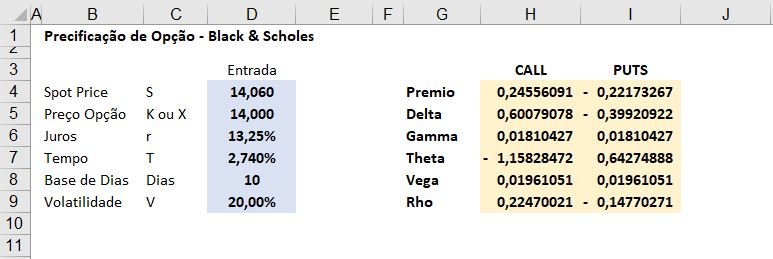
Vamos para as fórmulas, para calcular todas as Gregas da "Call", segue abaixo
Call - Opção de Compra
Prêmio - Call = 0,245560914336368
=D4*DIST.NORMP((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7)))-D5*EXP(-D6*D7)*DIST.NORMP((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))-D9*RAIZ(D7))ou em inglês
=D4*NORMSDIST((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7)))-D5*EXP(-D6*D7)*NORMSDIST((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))-D9*SQRT(D7))Delta - Call = 0,6007907823649
=DIST.NORMP((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7)))ou em inglês
=NORMSDIST((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7)))Gamma - Call = 0,0181042709959085
=(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))^2)/2)/RAIZ(2*PI()))/(D4*D9*RAIZ(D7))ou em inglês
=(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))^2)/2)/SQRT(2*PI()))/(D4*D9*SQRT(D7))Theta - Call = -1,15828471617406
=-(D4*(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))^2)/2)/RAIZ(2*PI()))*D9)/(2*RAIZ(D7))-(D6*D5*EXP(-D6*D7)*DIST.NORMP((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))-D9*RAIZ(D7)))ou em inglês
=-(D4*(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))^2)/2)/SQRT(2*PI()))*D9)/(2*SQRT(D7))-(D6*D5*EXP(-D6*D7)*NORMSDIST((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))-D9*SQRT(D7)))Vega - Call = 0,0196105066621741
=D4*(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))^2)/2)/RAIZ(2*PI()))*RAIZ(D7)ou em inglês
=D4*(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))^2)/2)/SQRT(2*PI()))*SQRT(D7)Rho - Call = 0,224700205088058
D5*D7*EXP(-D6*D7)*DIST.NORMP((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))-D9*RAIZ(D7))ou em inglês
D5*D7*EXP(-D6*D7)*NORMSDIST((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))-D9*SQRT(D7))Agora vamos para os cálculos das gregas para a opção "Put"
Put - Opção de Venda
Prêmio - Put = -0,221732668733628
=D5*EXP(-D6*D7)*DIST.NORMP(-(LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))-D9*RAIZ(D7))-D4*DIST.NORMP(-(LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7)))ou em inglês
=D5*EXP(-D6*D7)*NORMSDIST(-(LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))-D9*SQRT(D7))-D4*NORMSDIST(-(LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7)))Delta - Put = -0,3992092176351
=DIST.NORMP((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7)))-1ou em inglês
=NORMSDIST((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7)))-1Gamma - Put = 0,0181042709959085
=(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))^2)/2)/RAIZ(2*PI()))/(D4*D9*RAIZ(D7))ou em inglês
=(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))^2)/2)/SQRT(2*PI()))/(D4*D9*SQRT(D7))Theta - Put = 0,642748884069168
=-(D4*(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))^2)/2)/RAIZ(2*PI()))*D9)/(2*RAIZ(D7))+(D6*D5*EXP(-D6*D7)*DIST.NORMP(-(LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))-D9*RAIZ(D7)))ou em inglês
=-(D4*(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))^2)/2)/SQRT(2*PI()))*D9)/(2*SQRT(D7))+(D6*D5*EXP(-D6*D7)*NORMSDIST(-(LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))-D9*SQRT(D7)))Vega - Put = 0,0196105066621741
=D4*(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))^2)/2)/RAIZ(2*PI()))*RAIZ(D7)ou em inglês
=D4*(EXP(-((LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))^2)/2)/SQRT(2*PI()))*SQRT(D7)Rho - Put = -0,14770271044427
=-D5*D7*EXP(-D6*D7)*DIST.NORMP(-(LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*RAIZ(D7))-D9*RAIZ(D7))ou em inglês
=-D5*D7*EXP(-D6*D7)*NORMSDIST(-(LN(D4/D5)+(D6+((D9^2)/2))*D7)/(D9*SQRT(D7))-D9*SQRT(D7))Segue uma explicação rápida e simplificada sobre essas gregas.
Prêmio - é quanto o valor irá aumentar ou reduzir após o tempo estimado, validando se a opção (call ou put) está cara ou barata.
Delta - Reflete a variação relativa da opção ao preço, será a variação da opção para a variação do papel, exemplo: se o preço da opção variar 1 real o delta irá variar 0,83 centavos. Também podemos validar que ele terá 83% de probabilidade do preço que será exercido.
Gamma - Mede a aceleração do preço da opção.
Theta - Reflete a degradação do papel com o passar do tempo. Exemplo: se o valor resultar em -0,04, resultará o valor que a cada dia em que passa da venda do papel irá perder 0,04 centavos.
Vega - Mede a incerteza, sendo que a volatilidade alta terá uma incerteza alta, quando este valor está alto não compensa em ficar vendido em opção, ela é a sensibilidade da volatilidade.
Rho - Taxa de Juros, no caso acima se a taxa de juros subir 1%, será incrementado 0,03 centavos na sua opção (neste caso para a Call).

Esta técnica é bastante utilizada para operar opções na Bolsa de Valores.
Espero que tenham gostado desta aplicação no Excel
Gostou do artigo? Se sim curta e compartilhe com seus contatos!
Você tem uma outra técnica para precificação de opções? Deixe nos comentários deste artigo.
E ja conhece o meu novo curso online de Excel?
Abraços a todos
Fabio BALDINI
Frase do dia: "A vida é um eco. Se você não está gostando do que está recebendo, observe o que está emitindo" Auto: Buda
Agradecimento em especial ao Grande Mestre Davi Paraguai e ao Guilherme Yamazaki, por me proporcionar o curso de Bolsa de Valores e ao Valério Klug pela ótima explicação sobre o curso.



Link permanente
Olá Fabio.
Muito obrigado pelo maravilhoso artigo. Me ajudou muito.
Consegui reproduzir sua planilha para calcular o prêmio e as gregas. Precisei apenas fazer pequenos ajustes, como retirar o ponto da função DIST.NORMP e substituir o SQRT por RAIZ na fórmula do Vega da Put.
Gostaria de contar com sua ajuda para escrever uma fórmula para calcular a volatilidade implícita, a partir do prêmio que o mercado está pagando efetivamente.
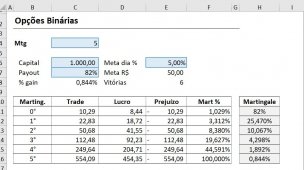
Atualmente uso o recurso “atingir meta” do excel, mas gostaria de ter isso calculado com uma fórmula.
Mais uma vez, muito obrigado.
Link permanente
Olá Fernando você tem o material disso? Que posso fazer um artigo resolvendo essa parte de aproximação por convergencia Monotonica,
Abraços
Link permanente
Boa noite,
Vi sua mensagem e fiquei muito interessado, gostaria de saber se tem desenvolvido algo novo, pois pelo que percebi, já tem um tempo essa postagem. Qualquer coisa, estou neste email: mateusbeloh@gmail.com, obrigado.
Link permanente
Olá Fernando, ainda não tenho, mas quero ver se posto alguma coisa ano que vem,
abraços
Link permanente
algumas fórmulas estão com erro.
Link permanente
Qual?
Link permanente
Gamma theta e vega. Os valores encontrados não batem com os seus.
Você poderia verificar, por gentileza? Muito obrigado por compartilhar.
Um abraço.
Link permanente
Olá Ricardo tudo bom, qual seria o seu cálculo? Abraços
Link permanente
Ricardo, atualizei as fórmulas, Abraços
Link permanente
Olá Ricardo, atualizei as fórmulas, Abraços
Link permanente
Olá Carlos você pode mostrar qual fórmula está com erro? Abraços
Link permanente
Muito Obrigado por compartilhar a planilha, Deus te abençoe.
Link permanente
Fábio, muito bom o artigo. Uma dúvida, o Excel descontinuou a formula DIST.NORMP para DIST.NORMP.N. Acredito que seja essa a diferença que o Carlos mencionou.
Abraço
Link permanente
Muito obrigado por compartilharem o conhecimento. Fiz o ajuste indicado pelo Fernando Amaral, acerca do tirar o ponto e funcionou perfeitamente. Só feras…..
Link permanente
Boa tarde professor baldini,
Agradecemos por sua contribuição, entretanto a possibIlidade de verificar se as fórmulas estão corretas, acabei de olhar no site https://opcoes.net.br/opcoes/bovespa/PETR4, o preço da PETR4 esta R$ 22,20 faltando 10 dia úteis para o vencimento, volatilidade implícita de 43,61% para call e 38,55% para put, para uma opção com strike R$ 23,03 consta:
CALL – preço 0,48 PUT – preço 1,20
– Delta 0,3645 Delta 0,6566
– Gamma 0,1857 Gamma 0,2057
– Theta -0,0352 Theta -0,0285
– Vega 1,7425 Vega 1,7058
Os valores ficam totalmente diferentes na sua planilha, com as formulas acima, exemplo, o valor da PUT está -0,11. Se o valor da ação esta acima do strike, a PUT terá mais valor do que a CALL.
No aguardo.
Link permanente
Olá Antonio você teria as fórmulas para eu atualizar no site? Abraços
Link permanente
Se eu tivesse as fórmulas já teria colocado aqui e só estou comentando porque tem algo errado, e o professor é você.
Link permanente
Prezado Antonio, você comparar um site com o meu, fica dificil, não sei se você sabe existe 6 tipos de Gregas que são eles B&S, Merton, Black, Asay, G&K e Commodity, favor descrever qual é o método que você gostaria para realizar a comparação.