▷ Machine Learning | K-Means no Excel

Olá seja bem vindo ao meu novo artigo!

O agrupamento k-means é um método de Clustering que objetiva particionar n observações dentre k grupos onde cada observação pertence ao grupo mais próximo da média.

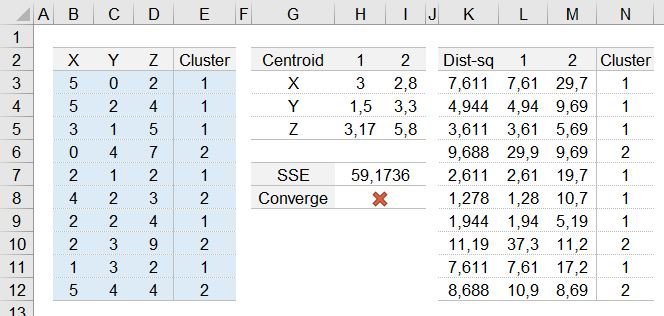
Neste exemplo, mapeado os pontos de X, Y, Z, foi atribuído um Cluster aleatório a cada elemento, inserindo o valor na coluna E.

Após definido o cluster (aleatório ou não) devemos efetuar os seguintes passos:

1° Passo - Calcular a média entre os centróides em relação aos clusters | Células H3 a I5

=MÉDIASE($E$3:$E$12;H$2;B$3:B$12)

ou em inglês

=AVERAGEIF($E$3:$E$12;H$2;B$3:B$12)

Para cada Eixo (X,Y,Z) e Cluster (1,2) deve adaptar a fórmula acima.

2° Passo - Calcular a Distância Euclidiana de cada ponto em relação os Centróides | Coluna L e M

=SOMAXMY2(B3:D3;$H$3:$H$5)

ou em inglês

=SUMXMY2(B3:D3;$H$3:$H$5)

Esta fórmula pode ser realizada de outra maneira, que segue abaixo

=SOMA(ABS($B3-MÉDIASE($E$3:$E$12;P$2;$B$3:$B$12))^2+ABS($C3-MÉDIASE($E$3:$E$12;P$2;$C$3:$C$12))^2+ABS($D3-MÉDIASE($E$3:$E$12;P$2;$D$3:$D$12))^2)

ou em inglês

=SUM(ABS($B3-AVERAGEIF($E$3:$E$12;P$2;$B$3:$B$12))^2+ABS($C3-AVERAGEIF($E$3:$E$12;P$2;$C$3:$C$12))^2+ABS($D3-AVERAGEIF($E$3:$E$12;P$2;$D$3:$D$12))^2)

3° Passo - Calcular a menor distância entre o cálculo do Cluster 1 e o Cluster 2 | Coluna K

=MÍNIMO(L3:M3)

ou em inglês

=MIN(L3:M3)

Com este resultado do menor valor será definido a nova posição do Cluster.

4° Passo - Definição da nova posição do Cluster | Coluna N

=SE(L3<M3;$L$2;$M$2)

ou em inglês

=IF(L3<M3;$L$2;$M$2)

Após esta nova definição, é verificado se houve alguma alteração entre a posição inicial para a posição atual.

5° Passo - Verificação de Convergência | Célula H8

=--E(ÍNDICE(E3:E12=N3:N12;0))

ou em inglês

=--AND(INDEX(E3:E12=N3:N12;0))

Caso o resultado seja positivo ou 1, não é necessário mais realizar iterações.

Para realizar a soma das distâncias (SSE), segue a fórmula abaixo, Célula H7

=SOMA(K3:K12)

ou em inglês

=SUM(K3:K12)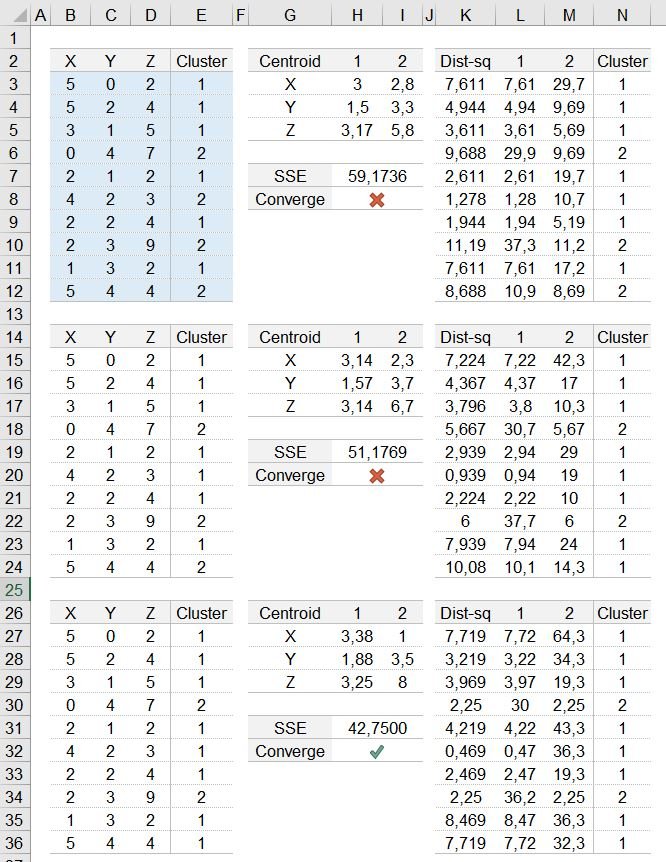

No exemplo acima, foi necessário somente 3 iterações para a convergência dos clusters, definindo cada elemento a o cluster mais "próximo".

K-Means | Exemplo Dinâmico

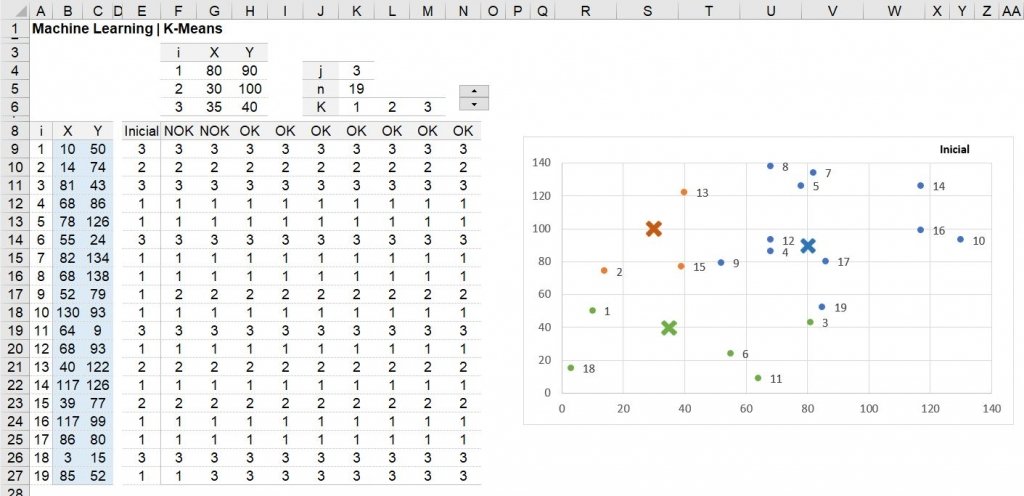
Com o método passo a passo visto acima, segue o modelo ajustado para uma coluna.

Nesta aplicação a atribuição do cluster inicial foi definido nas células F4 a H6, introduzindo 3 clusters (o elemento X do gráfico) com seus respectivos valores.

Para funcionar os cálculos dinâmicos serão necessárias algumas células auxiliares, que são elas:

Quantidade de grupos utilizado no modelo | Célula K4

=CONT.VALORES(F4:F6)

ou em inglês

=COUNTA(F4:F6)

Quantidade de registros na base | Célula K5

=CONT.NÚM(B:B)

ou em inglês

=COUNT(B:B)

Quantidade de grupos inseridos | Células K6 a M6

=SE(DESLOC($F$4;COLS($K$6:K6)-1;0)="";"";DESLOC($F$4;COLS($K$6:K6)-1;0))

ou em inglês

=IF(OFFSET($F$4;COLUMNS($K$6:K6)-1;0)="";"";OFFSET($F$4;COLUMNS($K$6:K6)-1;0))

Formação dos Grupos Iniciais | Coluna E

=ÍNDICE(DESLOC($F$4;0;0;$K$4;1);CORRESP(MIN(ÍNDICE(RAIZ((B9-DESLOC($G$4;0;0;$K$4;1))^2+(C9-DESLOC($H$4;0;0;$K$4;1))^2);0));ÍNDICE(RAIZ((B9-DESLOC($G$4;0;0;$K$4;1))^2+(C9-DESLOC($H$4;0;0;$K$4;1))^2);0);0);0)

ou em inglês

=INDEX(OFFSET($F$4;0;0;$K$4;1);MATCH(MIN(INDEX(SQRT((B9-OFFSET($G$4;0;0;$K$4;1))^2+(C9-OFFSET($H$4;0;0;$K$4;1))^2);0));INDEX(SQRT((B9-OFFSET($G$4;0;0;$K$4;1))^2+(C9-OFFSET($H$4;0;0;$K$4;1))^2);0);0);0)

Nesta etapa foi utilizado a distância euclidiana para a definição dos grupos iniciais.

Iterações | Coluna F a Coluna N

=ÍNDICE($K$6:$M$6;0;CORRESP(AGREGAR(15;6;ÍNDICE(ABS($B9-MÉDIASE(DESLOC(E$9;0;0;$K$5;1);$K$6:$M$6;DESLOC($B$9;0;0;$K$5;1)))^2+ABS($C9-MÉDIASE(DESLOC(E$9;0;0;$K$5;1);$K$6:$M$6;DESLOC($C$9;0;0;$K$5;1)))^2;0);1);ÍNDICE(ABS($B9-MÉDIASE(DESLOC(E$9;0;0;$K$5;1);$K$6:$M$6;DESLOC($B$9;0;0;$K$5;1)))^2+ABS($C9-MÉDIASE(DESLOC(E$9;0;0;$K$5;1);$K$6:$M$6;DESLOC($C$9;0;0;$K$5;1)))^2;0);0))

ou em inglês

=INDEX($K$6:$M$6;0;MATCH(AGGREGATE(15;6;INDEX(ABS($B9-AVERAGEIF(OFFSET(E$9;0;0;$K$5;1);$K$6:$M$6;OFFSET($B$9;0;0;$K$5;1)))^2+ABS($C9-AVERAGEIF(OFFSET(E$9;0;0;$K$5;1);$K$6:$M$6;OFFSET($C$9;0;0;$K$5;1)))^2;0);1);INDEX(ABS($B9-AVERAGEIF(OFFSET(E$9;0;0;$K$5;1);$K$6:$M$6;OFFSET($B$9;0;0;$K$5;1)))^2+ABS($C9-AVERAGEIF(OFFSET(E$9;0;0;$K$5;1);$K$6:$M$6;OFFSET($C$9;0;0;$K$5;1)))^2;0);0))

Validação das Iterações | Células F8 a N8

=IF(AND(INDEX(E9:E27=F9:F27;0));"OK";"NOK")

Este código foi desenvolvido para n variáveis e até 3 grupos (clusters), mas é possível adaptar para mais grupos, caso desejar.

Segue o funcionamento do K-Means Dinâmico no MS Excel.

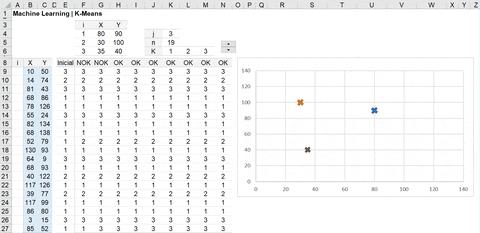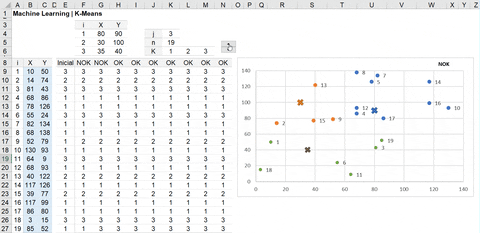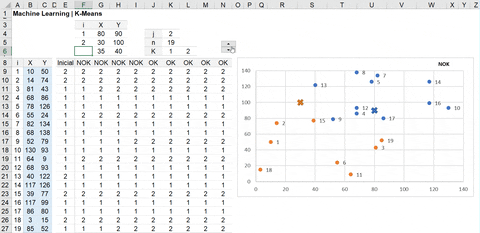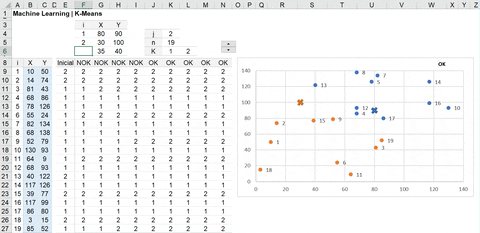
Espero que tenha gostado desse artigo!

Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.

Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.

E ja conhece o meu novo curso online de Excel?

Abraços a todos e até o próximo artigo!

Fabio BALDINI

Frase do Dia: "Quanto mais você sua no treinamento, menos sangra no campo de batalha." Autor: George S. Patton