Olá seja bem vindo ao meu novo artigo!
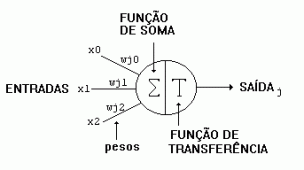
No reconhecimento de padrões, o algoritmo KNN ( k-vizinhos mais próximos) é um método não paramétrico usado para classificação e regressão.
Na classificação KNN , a saída é uma associação de classe. Um objeto é classificado pelo voto de pluralidade de seus vizinhos, sendo o objeto atribuído à classe mais comum entre os k vizinhos mais próximos ( k é um número inteiro positivo , geralmente pequeno), que será o objeto de estudo deste artigo.
Vamos aos cálculos
K = 1
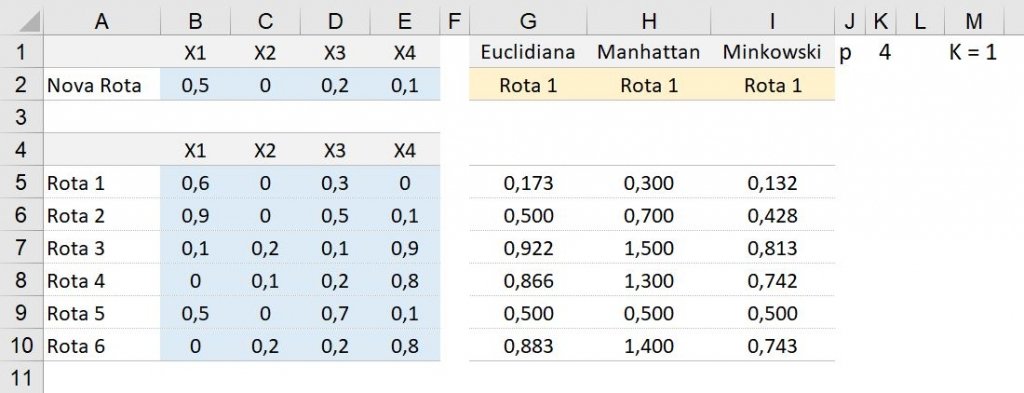
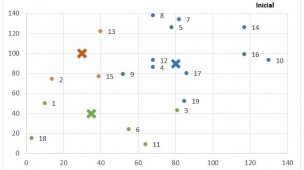
Com a imagem acima, temos seis rotas com seus respetivos valores (Latitude, Longitude, Qualidade da estrada, Preço do combustível) e adicionamos um novo destino. Esta técnica irá resultar em qual será o destino mais próximo em relação a todas as rotas listadas, neste caso a menor distância entre a nova rota será a Rota de Número 1.
Mas antes de iniciarmos o cálculo devemos conhecer três distâncias que será aplicado a esta técnica, são elas:
Distância Euclidiana | Células G5 a G10
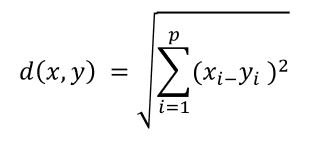
É a mais comum, considerada a distância geométrica (intuitiva) em um espaço p-dimensional
=RAIZ(SOMAXMY2($B$2:$E$2;$B5:$E5))ou em inglês
=SQRT(SUMXMY2($B$2:$E$2;$B5:$E5))Distância de Manhattan (City-Block) | Células H5 a H10
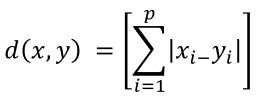
Esta distância é a média entre as dimensões, sendo o efeito de grandes diferenças são suavizados.
=SOMA(ÍNDICE(ABS($B5:$E5-B$2:E$2);0))ou em inglês
=SUM(INDEX(ABS($B5:$E5-B$2:E$2);0))Distância de Minkowski | Células I5 a I10
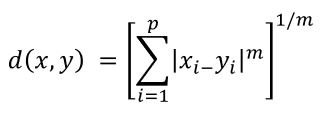
Esta distância é uma generalização da distância Euclidiana.
=SOMA(ÍNDICE(ABS($B5:$E5-$B$2:$E$2)^$K$1;0))^(1/$K$1)ou em inglês
=SUM(INDEX(ABS($B5:$E5-$B$2:$E$2)^$K$1;0))^(1/$K$1)Após as fórmulas das distâncias definidas em relação ao novo destino, é necessário achar a menor distância, consequentemente será o destino escolhido.
Segue a fórmula com o resultado da menor distância e o nome desta rota
=ÍNDICE($A$5:$A$10;CORRESP(1;ÍNDICE(ORDEM(G$5:G$10;G$5:G$10;1);0);0))ou em inglês
=INDEX($A$5:$A$10;MATCH(1;INDEX(RANK(G$5:G$10;G$5:G$10;1);0);0))O Fator K representa a quantidade de valores para realizar a escolha do menor destino, sendo o K=1, a primeira menor amostra é a resposta, o autor recomenda sempre escolher o K ímpar (1 ou 3 ou 5 ...), para caso der empate a classe que tiver o maior grupo é a qual o novo destino pertence
Segue um caso dinâmico com o Excel

Mas qual é o K ideal para o modelo? Segue a fórmula que faz a recomendação correta para o número correto K
=SE(MOD(LOG(CONT.VALORES(A6:A1250));2)=1;LOG(CONT.VALORES(A6:A1250));TRUNCAR(LOG(CONT.VALORES(A6:A1250));0)+1)ou em inglês
=IF(MOD(LOG(COUNTA(A6:A125));2)=1;LOG(COUNTA(A6:A125));TRUNC(LOG(COUNTA(A6:A125));0)+1)K=3 ou K=5
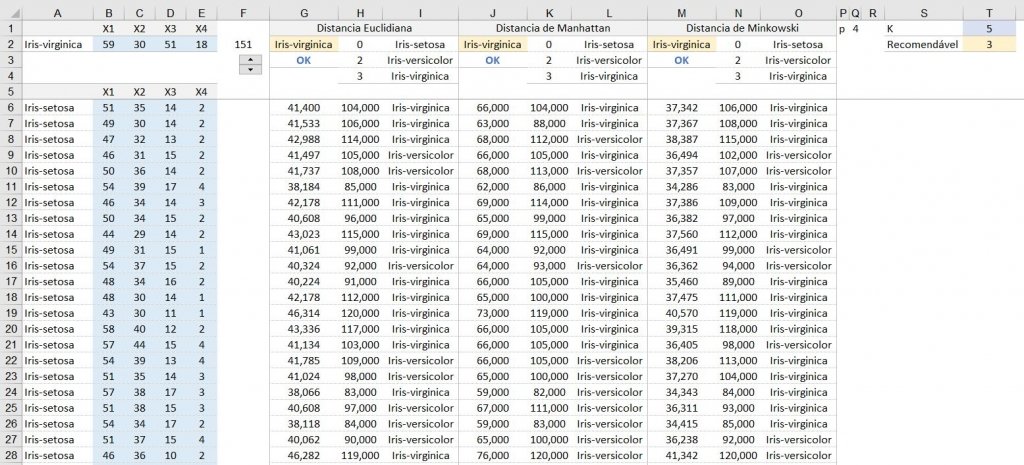
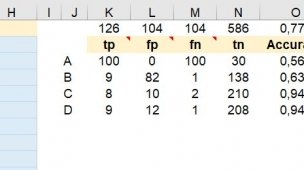
Quando se tem uma quantidade de amostra de dados significativos, é necessário utilizar o K>1, como neste exemplo acima, aplicado esta técnica a um conjunto de dados não linear IRIS.
Segue o link abaixo com os dados, para validação
https://archive.ics.uci.edu/ml/datasets/iris
Foi utilizado 80% dos dados de cada grupo para o treino e cálculo das distâncias e 20% para validação do KNN, onde teve a assertividade de 100%.
Para este caso adicionei mais colunas para suporte, mostrando o ranking da menor distância e qual classe o valor pertence, sendo a contagem dos 3 menores ou 5 menores distâncias em seus respectivos grupos.
A utilização de mais de uma amostra (acima de K>1) nos resulta uma escolha mais assertiva, pois o primeiro menor elemento pode estar mais próximo de um grupo, mas se verificar os outros 2 menores elementos (2° menor e 3° menor), este pode pertencer a outra classe, por isso a recomendação do K>1.
Vamos as fórmulas
Coluna de Rankeamento | Colunas H, K e N
=ORDEM(G6;G$6:G$125;1)+CONT.SE($H$5:H5;ORDEM(G6;G$6:G$125;1))ou em inglês
=RANK(G6;G$6:G$125;1)+COUNTIF($H$5:H5;RANK(G6;G$6:G$125;1))Coluna Classificada Crescente com o Nome do Grupo | Colunas I, L e O
=ÍNDICE($A$6:$A$125;CORRESP(MENOR(H$6:H$125;LINS($H$6:H6));H$6:H$125;0))ou em inglês
=INDEX($A$6:$A$125;MATCH(SMALL(H$6:H$125;ROWS($H$6:H6));H$6:H$125;0))Contagem dos Grupos | Células H2 a H4, K2 a K4 e N2 a N4
=CONT.SE(DESLOC(I$6;0;0;$T$1;1);I2)ou em inglês
=COUNTIF(OFFSET(I$6;0;0;$T$1;1);I2)Grupo com a classe que contem o maior grupo | G2, J2 e M2
=PROCV(MÁXIMO(H2:H4);$H$2:$I$4;2;0)ou em inglês
=VLOOKUP(MAX(H2:H4);$H$2:$I$4;2;0)Validação Final | Células G3, J3 e M3
=SE($A$2=G2;"OK";"NOK")ou em inglês
=IF($A$2=G2;"OK";"NOK")Espero que tenha gostado desse artigo!
Caso tenha alguma sugestão de outra técnica ou melhoria do conteúdo acima, poste aqui nos comentários.
Se gostou, curta e compartilhe este artigo para que todos saibam o que é possível fazer dentro do MS Excel.
E ja conhece o meu novo curso online de Excel?
Abraços a todos e até o próximo artigo!
Fabio BALDINI
Frase do Dia: "Substitua o medo do desconhecido por curiosidade" Autor: Dany Gokey